Numerical Precision - What Level of Accuracy is 'Good Enough'

In 1991, on the 25^th of February near the height of the Gulf War, a Patriot Missile Defense Battery deployed by the United States Army failed to intercept an Iraqi Scud missile. The Scud tore through a barracks of USA marines, killing 28 and wounding many more.

In 1996, on the 4^th of June, the USD$7 billion dollar Ariane 5 rocket exploded 40 seconds after lift off. Fortunately, this launch happened to be unmanned, but all on-board cargo and the rocket itself were lost.

But what do these two events have in common?

They were both a direct result of a lack of numerical precision.

Computers cannot store numbers in the sense we tend to assume they can. The reason behind this is that most decimals have an infinitely long representation in binary. For example, lets take a look at 0.1 - the most standard and widely used decimal. A computer actually stores it like this in binary:

The sequence goes on literally forever. That means that even if you were to dedicate your entire 1 TB hard drive to storing only the value 0.1, it would not be able to do so with 100% accuracy. We need to round the number off at some point along the chain. Let's investigate how this phenomenon affect the aforementioned disasters.

The Patriot battery had been operating for 100 hours straight since the last system boot when it attempted to intercept the Scud. Over this 100 hour period, the internal clock of the interceptor guidance system had drifted by 0.34 seconds. When comparing this to the approach speed of the Patriot intercepting missile relative to the Scud, 0.34 seconds results in a miss of a distance greater than 630 meters.

How did the clock drift? Why does a clock drift?

In this case, the internal Patriot launcher clock measured the time in tens of seconds, and the Patriot Interceptor Missile calculated the current time in seconds by multiplying this by a factor of one tenth. Due to the decimal 0.1 being a non-terminating (never ending) binary expansion, and the calculation's result being stored in 24 bit fixed point register, only 24 bits of accuracy were maintained each calculation.

This might seem insignificant. For most applications it would be! Let's have a closer look at how this rounding error yielded a clock time that was out by 0.34 seconds. The number 1/10 can be represented as the infinite series:

(1/2)⁴ + (1/2)⁵ + (1/2)⁸ + (1/2)⁹ + ...

As demonstrated earlier in this article, the binary expansion of this infinite series is 0.0001100110011001100110011001100110011001100110011001100...

The hardware in the Patriot Missile could only store 24 bits of this number though, so it represented the above fraction as 0.00011001100110011001100, which means the error introduced is made up of the value represented after the 24^th entry in the series. When converted back to decimal, this is roughly 0.0000000945. Multiplying this through by the number of times that Patriot made this rounding error (every tenth of a second for about 100 hours) we get:

0.0000000945×100×60×60×10 = 0.3402 seconds of error

Given that a Scud reaches speeds just shy of 1.8 km/s, this means it had traveled well over half a kilometer in this time.

The Ariane 5 experienced a similar error, but more abrupt. The internal guidance system of the rocket stored its horizontal and vertical velocities as 64 bit floating point numbers. However, when trying to quantify these relative to its launch platform the numbers were converted to a 16 bit signed integer, which has a maximum value of 32768. At the time of failure, the number that was being converted exceeded 32768 and caused the guidance system to misfire the booster rockets. This deviated the rocket from its intended path so violently that it broke apart due to mechanical stress.

Had 32 bits of storage been assigned to the stored signed integer, the rocket would not have failed.

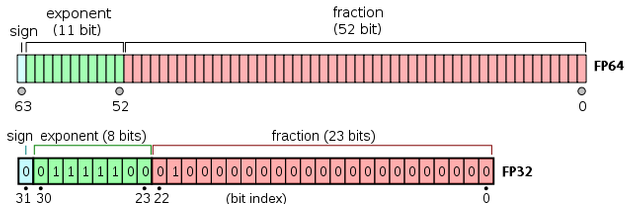
You might be wondering at this stage how this is even remotely relevant to everyday computer users. In fact, you would be correct in assuming that for an everyday user, it isn't. Modern computer hardware development (especially GPU development) is driven almost exclusively by the gaming industry, where 32-bit precision has become the standard. This is often referred to as 'single precision', or FP32, and with regard to accuracy that is actually overkill in every sense of the word. No-one playing a shooter is going to be able to tell the difference between a colour (or a position) stored in 32-bit vs 64-bit (FP64 - double precision).

The numerical accuracy of a GPU or CPU starts to matter when we try and do hard science, like intercepting a missile or launching a rocket. Numerical errors in 32-bit rapidly accumulate when performing literally trillions of FLOPS due to a combination of rounding, approximations and truncation errors. For example, modelling the Milky Way (an ongoing project by the BOINC initiative at Berkeley) cannot be done in 32-bit precision to a level of accuracy that is useful. In my PhD research, modelling the human brain for any reasonable timescale also cannot be done in anything but 64-bit precision, as the compounding errors in 32-bit are so significant that they alone determine whether the virtual brain tissue slice being simulated is 'alive' or 'dead'. As we get further into the age of computational research, I predict a slow phasing out of FP32 centred hardware as it simply becomes unable to keep up with most high-performance compute tasks other than gaming.

Computers are not perfect - and unless we see some groundbreaking overhaul of their fundamental architecture they never will be. But that's ok! We just need to be sure that we are aware of their limitations, and what is 'good enough'.

Generally speaking, it would be ill advised to launch a rocket with hardware less accurate than what you may use to play Call of Duty.