More humans currently alive than dead - DEBUNKED!!!!!!
Someone once told me, as one of those interesting facts that you wouldn’t believe, that more humans were alive than dead. Due to exponential growth, they claimed, more humans were currently roaming the planet than all of the people summed up who had ever roamed the planet before.

This statement has my BS senses tingling, and it would be nice to ballpark the number to see if the figure could even have a chance of being true. To do this, I decided to model some exponential growth to quickly check. Unfortunately, models of exponential growth are really sensitive to certain factors over long periods of time. For me, my biggest worry was that I could model the growth as a constant growth rate over something like 50,000 years of human existence, but probably for most of that time, humans were not reproducing nearly as quickly as they have been in, say, the past 1000 years.
Therefore, I wanted to start by looking at a much more restricted range, where we have good historical estimates of population size. I’ll start with the year 1500, where a number of sources put the world population around a measly 500,000,000 (0.5 billion) people. Okay, we’ll also need to know the current population, which is about 7,500,000,000 (7.5 billion), which is 517 years later. Finally, we’ll need to have some estimate of average human lifespan across that time. I think for these purposes, we should be extra conservative and say 80 years.
Now let’s do some math. We’re going to use differential equations, which is the art of modeling variables and how they change over time in the same equation. My model is going to be really, really simple. I’m going to say that the change in population over a tiny increment in time is equal to current population multiplied by that population’s growth rate. This might almost feel too obvious because that’s how we think of rates already. If you’re earning some interest in your bank account, you intuitively already understand that the amount of money you can expect to earn in some period of time depends on the interest rate and the starting amount that you have in the bank account. This is just the same thing applied to population growth. Math has a pretty standard notation to formulate this abstractly. t is time. x is people. r is growth rate.
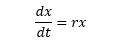
In this equation, dx/dt means “a tiny change in population per some tiny change in time.” We’re saying that this tiny change in population per tiny change in time can be determined by multiplying the rate by the current number of people.
Here’s the cool part: we can formulate this equation to solve for a function that will tell you the population at any point in time after some starting time. We can do this using the tools of calculus, which are all logically derived, but let’s leave those derivations for another time. Right now, let me just show you how to use those tools as shortcuts for solving this problem. I’ll show you the steps, and I encourage you to learn these tools from the many awesome online resources if you’re interested in knowing more.
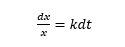
In this first step, I’ve used a sort of pseudo, non-rigorous algebra to bring the “x” components together. You can think of this sort of as dividing both sides by “x”, and multiplying both sides by “dt” to reorganize the equation. To be honest, I don’t really know why everyone talks about calculations like this as “non-rigorous” because this is typically the way it is taught to set up your differential equation. Now we are going to do something called “integration” on both sides.
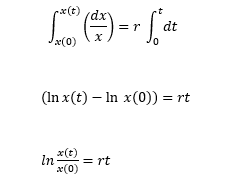
Solving this in terms of x(t)…
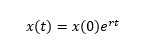
####If these steps seem mysterious to you, don’t be discouraged; they should!
A lot of these shortcuts and notational rules took a tremendous amount of logical effort on behalf of mathematicians to create these incredible tools that save huge amounts of time in solving these equations.
For instance, I have memorized a rule, that integrating 1/x will give me ln(x), and I don’t need to logically derive that rule every time I use calculus. In a similar way, I know rules for working with logarithms, rules of algebra, and rules of integration.
Integration is similar to summing things over some variable (e.g. time), and for our purposes, it ends up being sort of the opposite of figuring out these small changes in time, so it helps us in this case to express an equation in terms of specific points in time.
. A simple example might help. Imagine that you know a car is moving at a rate of one meter per second, but you’re more interested in knowing the car’s position in say, 3 seconds. Now you probably already immediately know the answer is 3 meters further than it’s starting point, but I want to show you the steps. You could write a function to express the rate of the car:
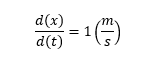
Notice that in this case, the small changes in x do not depend on the prior values of x; the rate is constant. Now we can solve like we did before.
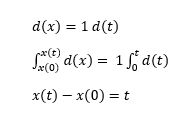
Solving in terms of x(t)…
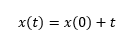
If we plug in that the starting position of the car was 0 and then add the value of t, which is 3 seconds, then we know that the position after 3 seconds is 3 meters. Hopefully that gives you an intuition for why we are solving the equation this way. Now back to our population problem!
For our population problem, the first step is to estimate the growth rate. For this, I just plug in those initial values that I had come up with and solve for r.
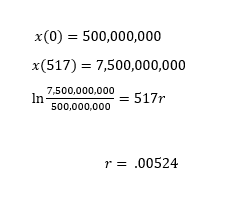
With the rate solved, I can model a function of growth from the year 1500 to 2017 that would allow me to estimate the population for any particular year. When I plot x(t), I get a curve that looks like this:
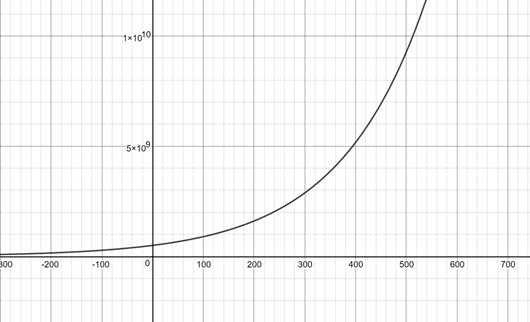
Now, I’m not really interested in estimating how many people lived at a certain point in time from 1500 to 2017. I’m interested in summing up all the people who died from 1500 to 2017. Let’s integrate this curve!
I’ll start with my equation:
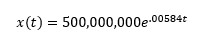
And integrate
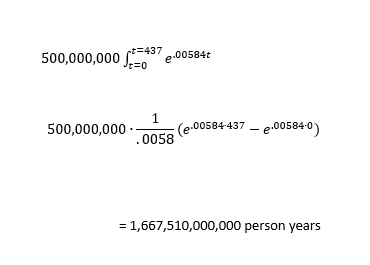
Now we need to divide that by our estimate of the average lifespan, which was 80 years, in order to get the total number of people alive during this time-span.
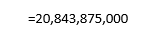
Last step is to subtract the living from that!
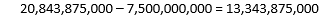
That’s almost twice as many dead people to alive people already, and that’s only calculating from the Renaissance! Therefore, this statement about more alive people than dead people is almost definitely wrong. Hopefully, this exercise gives you some impression of how we can use some direct analytical thinking and some cool mathematical tools to debunk some of those wild statements that people are throwing around!
Photo credit: Lars Curfs
While I agree that this approximation works well, your function for predicting the population (especially for humans) is rather generic. I am curious if you have thought about the potential of this argument had you extended this to be capable of holding multiple dynamic variables to more accurately predict populations? Either way the outcome would still produce a value that is much larger than the current population. I quite enjoyed the read, thank you for sharing! I reposted so more people can see it!
You're totally right. I would never use this try to get an accurate function for population growth, and there are much more refined population growth models out there. The most important variables I can think of are changing rates of reproduction and changing lifespans. I tried to choose a time period after the biggest plagues and choose a very conservative lifespan, so that I could be fairly confident that I wasn't over-estimating...but there are other factors as well. Population growth rate likely increased a lot after the industrial revolution. I was motivated to take this approach by trying to think of a way that I could quickly refute the next person who made this claim to me using a napkin and a phone calculator.
Well it is still done very well. If it would be okay with you, I would like to ask permission to be able to link this as a potential resource for when I see people make similar claims.
Of course! Thanks.
Makes me think of the part of Bill Bryson's book At Home where he talks about the way that English churches seem to be sunken into the ground around them, because of all the built up matter of buried bodies from the past 1000+ years.