Geometry - Distance calculations with the hesse normal form
Hi everyone :)
The hesse normal form is a special equation, which is used in analytical geometry. It describes a straight line/plane in an Euclidian space through the distance to the coordinate origin and a normed and orientated normal. Today I want to show you, how you can easily use it to calculate the distance of a point to a plane. I use the hesse normal form in the cartesian equation form for this:
our general form of the calculation
Where does this general form come from?
If you choose a vector of the length one for the normal of a plane, the plane equation looks like this:
if n1 * x + n2 *y + n3*z =a a cartesian plane equation of the plane E, then the normal unit vector
n0 = 1 / √(a1 + a2 + a3 ) * (a1/a2/a3)
with a (a1/a2/a3) and the formular of before for the distance "d" of a point to a plane the last equation on the picture above, with which we are going to work now.
Example:
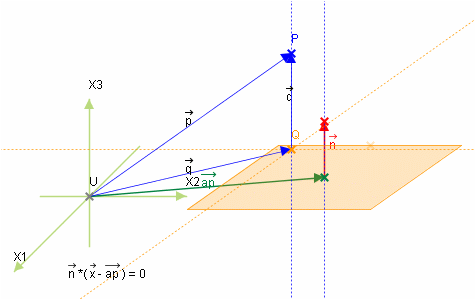
with this picture you can see how the equation works
We have a plane with the following plane equation:
p: 12x1 + 6x2 - 4x3 = 5
And we have a random point:
a (1/2/3)
What we have to do now?
As we already have the general form of the calculation, it is as easy as you think:
Just put in the given information:
1. Put the point "a" into the cartesian equation:
12 * 1 + 6*6 - 4*2 - 5
2. Find out the normal of the plane:
(12/6/-4)
3. Calculate the vector amount of the normal
n = √ (12 ² + 6 ² + (-4) ² )
4. Divide the cartesian equation with the inserted point by the vector amount of the normal
distance d = ( 12 * 1 + 6*6 - 4*2 - 5 ) / √ (12 ² + 6 ² + (-4) ² )
5. Our result is:
35 / √196
= 35/14
= 2,5
Answer: Our distance d = 2,5
Conclusion
As we have the equation to calculate the distance between a point and a plane, we can easily put in the given information about the point and within a few steps we get the right result, if we haven't put it in wrong or left out something.
Have a nice day :)
Source
Texthttps://en.wikipedia.org/wiki/Hesse_normal_formhttps://www.frustfrei-lernen.de/mathematik/hessesche-normalform.html (translated)http://mathworld.wolfram.com/HessianNormalForm.htmlErnst Klett Verlag, Lambacher Schweizer Seite 283-284 ( 1.Auflage) (translated)
Pictures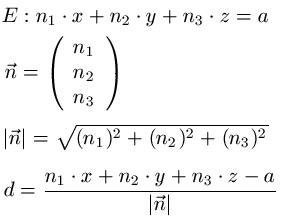
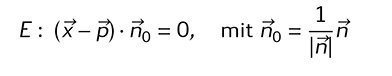
Upvoted and RESTEEMED :]
Thanks :)
Congratulations @aximot, this post is the seventh most rewarded post (based on pending payouts) in the last 12 hours written by a User account holder (accounts that hold between 0.1 and 1.0 Mega Vests). The total number of posts by User account holders during this period was 1880 and the total pending payments to posts in this category was $1789.22. To see the full list of highest paid posts across all accounts categories, click here.
If you do not wish to receive these messages in future, please reply stop to this comment.