Chaotic Systems

Chaotic systems are a part of chaos theory, which is a branch of mathematics.

The First Step in Creating Chaos

The first step in creating a chaotic system is creating a system highly sensitive on initial conditions. This excludes any linear relationships.

Imagine an asteroid sitting on an imaginary line connecting two planets. You know it will also fall in the direction of the greatest gravity. The closer its initial position is to one planet, the faster it will accelerate and the slower it will be when it impacts. That is easily predictable. There will be a point where it falls towards neither planet, and predictably on each side of the point it will fall towards that sides planet. The outcome doesn’t really change much based on initial position. The closer the asteroid starts, the slower it is when it lands. We need to make it more complex.

Now imagine a more common situation where the asteroid is not sitting on that line. This means that the asteroid most likely won’t travel in a straight line to a planet and may even miss it entirely. This means that in many spots the asteroid could slingshot around one planet and land on the second.

At some starting positions it will go from being close to one planet to the other hundreds or even thousands of times. In some rare circumstances it may even never land at all, going back and forth forever. Since gravity changes with the square of the distance, any small change will be amplified. Since the asteroid orbits so many times it will be amplified again and again. Any infinitely small change in starting position could mean it ends up on the opposite planet. This makes anything that happens at these points is basically impossible to predict. This is called a divergence of outcomes, and places like this are where chaos is born. However, that is not the only requirement for a system to be chaotic. This is just the first of three requirements, for the system to be heavily reliant on the initial conditions.[1]

---

source

---

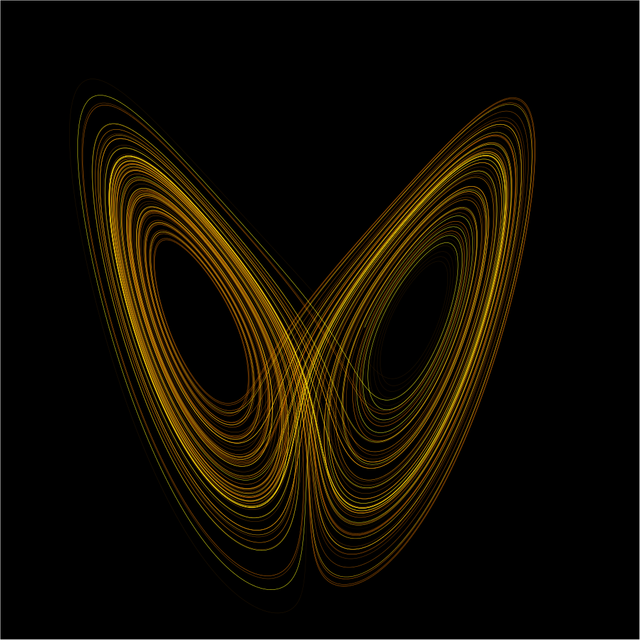
In this the planets are attractors, but not strange attractors. Chaotic systems are never able to come to a rest, while the asteroid can impact a planet in this example. Strange attractors cause the system to rest in some sort of dynamic equilibrium. A property of strange attractors is that you will never know where exactly on the attractor the system will be.[2]

The Second Requirement

There was a problem with the first example. The system must be topologically mixing to be chaotic. Topologically mixing means that the system may look and act just like another of the same system, but very small differences can cause it to suddenly change. In other words the paths of very different outcomes can look very similar.

Imagine a pendulum swinging back and forth. The smallest push will change the system forever, but will not have much effect. This system needs something else to become topologically mixing.

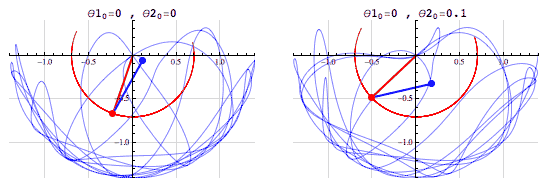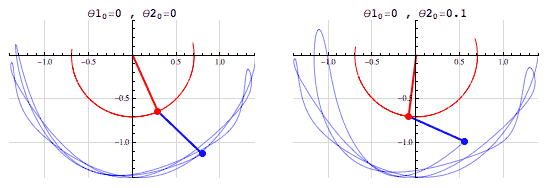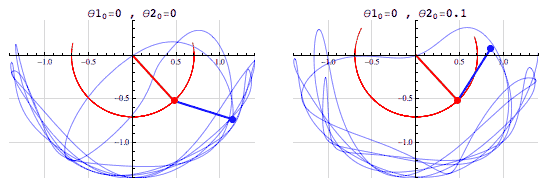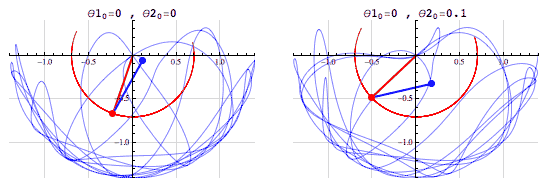
Now imagine a system with two pendulums. A two pendulum system will act in ways a single pendulum system will not. For example in a double pendulum system the bottom pendulum may have enough power to jump over the top pendulum. Since the position and velocity of each pendulum affects the other, a feedback loop occurs.Since in many places a pendulum is on the edge of jumping over the other, two systems that look very similar can quickly diverge. This will happen with the system infinitely and it will eventually come arbitrarily close to every point.[3]

---

source

---

Since the system has many different places where it diverges quickly after looking basically identical we can say it is topologically mixing. This system is a chaotic system, but I will use another example to go over the last requirement.

---

The Last Requirement

The last requirement is dense periodic orbits. Periodic orbits means that there exists orbits within the system that repeat. Dense periodic orbits means that the stable states and the unstable states are so close together that it is impossible to tell them apart and that they might diverge at any point in time. This means that it is impossible to figure out prior states of the system.

Imagine a small town with one grocery store. As people leave the store can no longer make a profit and shuts down. More people leave and demand for a grocery store increases, so another company decides to build one there. This attracts more customers and people move in, but some people were already in the process of leaving. This starts the cycle again. The specific amount of people change, but the general system remains. Maybe at one point the system reaches an equilibrium where the same amount of people come and go every time. This will almost certainly be broken at one point or another. Maybe somebody moves out for a reason other than the grocery store closing. That would send the system into a spiral of uncertainty.
[4]

---

This last system is an example of a chaotic system. It has two strange attractors, one grocery store or no grocery stores but it never stays there for long. It will eventually reach every possible state. Chaotic systems exist throughout nature. Understanding them might give an insight into them and help us predict what they will be more likely to do.

---

Want to learn more science? Subscribe and Upvote!

[1]source
[2]source
[3]source
[4]source