Los Autómatas Finitos Deterministicos (Parte II)

Fuente: Foto tomada en mi viaje a Argentina, en la ciudad de Puerto Madryn, en octubre del 2012.

Este post es la continuación del post Los Autómatas Finitos Deterministicos (Parte I) el cual es parte del curso de adiestramiento "Introducción a las Redes de Petri". Hoy hablare un poco de los grafos, sus usos y algunas características. Comenzemos...

Grafos

Informalmente, un grafo es un conjunto de puntos, algunos pares de los cuales están unidos por líneas. La naturaleza de los puntos y las líneas no tiene importancia, lo que interesa es la relación de incidencia entre unos y otros, es decir saber cuáles son los extremos de cada línea, y de qué líneas es extremo cada punto. En nuestro quehacer diario estamos rodeados de ejemplos que se modelan mediante grafos, a pesar que no pensamos en ellos como tales. Por ejemplo, las carreteras o avenidas, las líneas telefónicas, redes eléctricas bien sea de nuestra casa, o de la urbanización o ciudad o pueblo, los organigramas empresariales o de cualquier institución de una empresa, nuestros árboles genealógicos, etc.

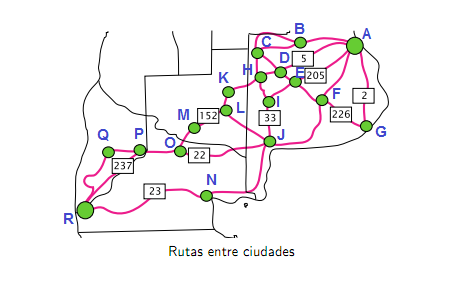
Más formalmente definiremos un grafo sigue:
Definición 2. Un grafo es una estructura G=(V,E) que consta de:

1. un conjunto finito V de elementos llamados vértices (o puntos, o nodos),
2. un conjunto finito E (disjuntos de V) de elementos que llamaremos aristas (o líneas, o arcos), y
3. una función que a cada arista le hace corresponder un par (ordenado o desordenado) de vértices, que se consideran los extremos de la arista.

Podemos entonces nombrar algunas consideraciones acerca de los grafos:

1. Si los extremos de una arista coinciden: tal arista se denomina bucle o lazo.
2. Si dos aristas diferentes tienen el mismo par de extremos, se dice que tienen aristas múltiples.
3. A los grafos que tienen aristas múltiples se les llama multigrafos.
4. Si los extremos de cada arista son un par desordenado de vértices {u,v}, se tiene un grafo ordinario (o no orientado).
5. Si en los extremos de cada arista son un par ordenado de vértices (u,v), se tiene un grafo dirigido (o digrafo).
6. Un vértice y una arista son incidentes si el vértice es uno de los extremos de la arista.
7. Dos vértices u y v son adyacentes si hay una arista que los tenga como extremos.
8. El grado de un vértice v de un grafo es el número g(v) de aristas incidentes con él.
9. Si g(v)=0 se dice que v es un vértice aislado.
10. En el caso de los digrafos se distingue el grado saliente de v (número de aristas de las cuales v es origen) del grado entrante (número de aristas de las cuales v es extremo).
11. Un subgrafo de G=(V,E) es un grafo H=(W,F) tal que W subconunto de V y F es subconjunto de E.
12. En un grafo simple cada arista tiene un par (no ordenado) de vértices diferentes como extremos (no hay bucles). Además, para cada par de vértices hay a lo sumo una arista que los tiene como extremos.
13. Si una arista tiene extremos u y v no hay ambigüedad en denotarla uv.
14. Un grafo simple es regular si todos sus vértices tienen el mismo grado. Si el grado común es k se dice que el grafo es k-regular.
15. A los grafos 3-regulares se les llama también grafos cúbicos.
16. Un grafo se dice completo o clique de n vértices al grafo K con n vértices y (n(n-1))/2 cantidad de aristas, cada una de las cuales conecta un par de vértices diferentes.
17. Un grafo G=(V,E) se dice que es k-partito si el conjunto de vértices V puede particionarse en k>1 subconjuntos disjuntos, que llamaremos bloques, tales que ninguna arista de G tenga sus dos extremos en el mismo bloque.
18. Si cada vértice de un bloque es adyacente a todos los vértices de los bloques restantes, entonces se dice que es k-partito completo.
19. Los grafos 2-partitos se llaman también bipartitos.

Abdul Abner Lugo Jiménez
Twitter: @abdulmath
Instagram: @abdulmath
Facebook: https://www.facebook.com/alugo1978
Telefono: +58-414-9719116
email: [email protected]