Run the Math: Calculus 1: Limits
Run the Math
Limits
By Bryan Bartlett
Previous-----Index-----[Next]
Answers to Previous Lecture
f(x) = cos(x) is a function, but it is not 1 to 1. It is periodic, so it repeats at every 2π.
f(x) = x5 + 4x2 - 3 is a function, but it is not 1 to 1. f(x) can equal 0 at 3 different values for x
y3 = x - 1 From the graph, we can see that it passes the horizontal test for 1 to 1, but what about the vertical test? Eyeballing it, we cant tell if it passes the vertical test, so we will need to analyze it mathematically. Now, if you take a positive number and square it, you get a positive. But if you do same to negative, you also get a positive. If you take the square root of something in an equation, you have to add ± to the front of it to show there are two different solutions . This is the same when you take the nth root of any number, provided n is even. But if it is odd you dont! A positive number cubed is always positive, and a negative number cubed is always negative. so, we can say with certainty that y3 = x - 1 ≡ y = 3√(x-1). y has only 1 value for each value of x, so it is a function, and it is 1 to 1
As complicated as this looks, taking it a bit at a time can be helpful. Using our function operations, ((hg + g2)/2-f)(x) ≡ (h(x)g(x) + g(x)g(x))/2 - f(x)
h(x)g(x) = (x + 3)(x - 3) = x2 - 9
g(x)g(x) = (x - 3)(x - 3) = x2 - 6x + 9
so, h(x)g(x) + g(x)g(x) = x2 - 9 + x2 - 6x + 9 = 2x2 - 6x
(2x2 - 6x)/2 = x2 - 3x
x2 - 3x - f(x) = x2 - 3x - x2 = -3x
so, ((hg + g2)/2-f)(x) = -3x(g ◦ h)(x) = g(h(x)), and h(x) = x - 3, so (g ◦ h)(x) = g(x-3). if g(x) = x + 3, then g(x-3) = x - 3 + 3 = x. therefore (g ◦ h)(x) = x. Extra note! This means that h is the inverse function of g!
(f ◦ f-1)(x) = (f(f-1)(x)) = f(3√[(x - 4)/3]) = 3(3√[(x - 4)/3])3 + 4
= 3([(x - 4)/3]) + 4
= x - 4 + 4
= x
Concept of Limits
Whenever you see a problem dealing with limits, you will see it in the format
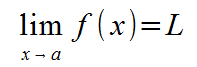
you are dealing with a limit problem. This equation means that the value of f(x) will approach L as x approaches a. Where this comes into importance is equations where f(x) is undefined at x=a, like 1/x is undefined when x = 0, and (x2 + 3x + 2)/(x+1) is undefined when x = -1. By taking limits, we can see what happens at points where normal calculations do not work. In our examples, 1/x approaches infinity as x approaches 0 but (x2 + 3x + 2)/(x+1) approaches 1 when x approaches -1
Limits become useful in calculus, because it forms the basis of derivatives, which is about finding the equation for the slope of a formula at a given point. If we had a line, we could calculate its slope using the "rise over run" method. that is.. the change of y over the change of x equals the slope. If we used 2 points x and x + h in the formula f(x), we could write this as follows:
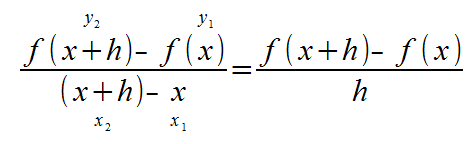
This is called the difference quotient. But what if you want to know the slope of the line at exactly the point x? This would be when h=0. But h = 0 is undefined in our equation. This is where limits come in.
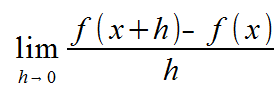
This formula gives you the equation for the tangent line of a formula, which is actually what the definition of what a derivative is! More about this in later sections!
Calculating Limits
When attempting to calculate limits, the idea is to manipulate the formula in a way that removes whatever is causing the formula to be undefined. We have a few powerful limit theorems to deal with this. Let f and g be functions, and let c be some constant...
This tells us that there either 0, or 1 limit given any value a. You will never have multiple limits. This is a consequence of the definition of a function.
This means simply, if f(x) is a constant, then its limit as x approaches anything is that same constant. You can see easily that if f(x) = 5, as x approaches any real number, the value f(x) will always be 5.
if
and
, then all the following are true
You can remove a scalar multiplier from the formula, and apply it to the calculated limit.
If you have two functions added or subtracted together, you can calculate their limits separately, and add or subtract the limit caclulations at the end.
If you have two function multiplied together, you can calculate their limits separately and multiply the limit calculations at the end
if M≠0
Provided that g(x) limit does not equal 0, you can calculate each limit individually, then use the quotient on the limit calculations. If L ≠ 0 and M = 0, thendoes not exist.
Note: Imagine a function f(x) and g(x), where both are 0. This means that either f(x) = g(x) = 0 OR f(x) = g(x)h(x), where h(x) is some other function. In both cases you will have a limit of either 1 or h(x).
Example: We define if a function is continuous at a point a provided all the following are true Continuity Theorems: a. cf is continuous 2 If f and g are If f is continuous at a and g is continuous at f(a), then g◦f is continuous For the following formulas, state if a limit exists, and if so, what is it
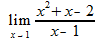
In this example, you can see we can not simply put x = 1 to solve, as that gives us a value of 0 at the bottom. But we can look at what the top does. If it's limit when x approaches 1 is also 0, then we can say that the limit exists. x2 + x - 2 equals 0, so there must be a limit. We need to try to simply this problem where x ≠ 1. We can do this because the equation never actually asks us for what it is equal to when x = 1, instead only wanting to know what it is when you get arbitrarily close to x = 1. so...
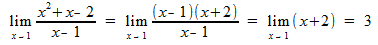
Continuity
We say that f(x) is continuous over an interval if it is continuous at all points in that interval.
1 If f and g are continuous functions over the same interval and c is a constant,
b. f+g and f-g are continuous
c. fg is continuous
d. f/g is continuous, where g(x)≠0Assignment


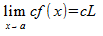

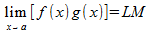
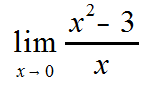
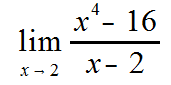

This is a really good explanation! I was looking over my limits notes studying for my upcoming final when I saw this. I just have to ask, would you like us to comment the answers or just keep it on some paper? Anyways nice post!