RE: Quantum Universal Triangular Tetrahedral YHVH Bible Codes 153 Part 2 God's Signature
Cyclosilicates (Ring Silicates)
If two of the oxygens are shared and the structure is arranged in a ring, the basic structural unit of the cyclosilcates or ring silicates. Shown here is a six membered ring forming the structural group Si6O18-12. Three membered rings, Si3O9-6, four membered rings, Si4O12-8, and five membered rings Si5O15-10 are also possible. A good example of a cyclosilicate is the mineral Beryl - Be3Al2Si6O18.
Nanoscalemetrology Soft Matter Dynamics
A Quasicrystal or quasi-periodic crystall is matter formed atomically in a manner somewhere between the amorphous solids of glasses (special forms of metals and other minerals, as well as common glass) and the precise pattern of crystals. Like crystals, they contain an ordered structure, but the patterns are subtle and do not recur at precisely regular intervals. They appear to be formed from two different structures assembled in a nonrepeating array, the three-dimensional equivalent of a tile floor made from two shapes of tile and having an orientational order but no repetition. Although when first discovered such structures surprised the scientific community, it now appears that quasicrystals rank among the most common structures in alloys of aluminum with such metals as iron, cobalt, or nickel. While no major commercial applications yet exploit properties of the quasicrystalline state directly, quasicrystals form in compounds noted for their high strength and light weight, suggesting potential applications in aerospace and other industries.

Electron microscope and quasicrystals?
It is a versatile tool that can probe many important aspects of the structure of matter. Low-resolution scanning electron microscopy magnifies the shapes of individual grains. Symmetries of solid grains often reflect the internal symmetries of the underlying atomic positions. Grains of salt, for example, take cubical shapes consistent with the cubic symmetries of their crystal lattices. Quasicrystalline aluminum-copper-iron has been imaged using a scanning electron microscope, revealing the pentagonal dodecahedral shape of the grains. Its 12 faces are regular pentagons, with axes of fivefold rotational symmetry passing through them. That is to say, rotations about this axis by 72° leave the appearance of the grain unchanged. In a full 360° rotation the grain will repeat itself in appearance five times, once every 72°. There are also axes of twofold rotational symmetry passing through the edges and axes of threefold rotational symmetry passing through the vertices. This is also known as icosahedral symmetry because the icosahedron is the geometric dual of the pentagonal dodecahedron. At the centre of each face on an icosahedron, the dodecahedron places a vertex, and vice versa. The symmetry of a pentagonal dodecahedron or icosahedron is not among the symmetries of any crystal structure, yet this is the symmetry that was revealed in the electron microscope image of the aluminum-manganese alloy .
Fivefold symmetry axes are forbidden in ordinary crystals, while other axes, such as sixfold axes, are allowed. The reason is that translational periodicity, which is characteristic of crystal lattices, cannot be present in structures with fivefold symmetry. High-resolution electron microscopy magnifies to such a great degree that patterns of atomic positions may be determined. In ordinary crystals such a lattice image reveals regularly spaced rows of atoms. Regular spacing implies spatial periodicity in the placement of atoms. The angles between rows indicate rotational symmetries of the atomic positions. In a high-resolution electron microscope image of quasicrystalline aluminum-manganese-silicon, parallel rows occur in five sets, rotated from one another by 72°, confirming that the fivefold symmetry suggested by the shape of the pentagonal dodecahedron grain reflects a fivefold symmetry in the actual placement of atoms.
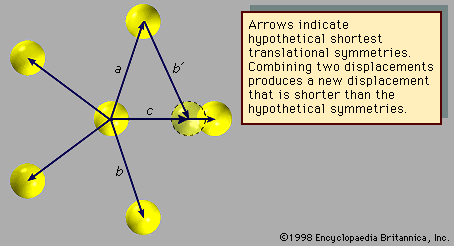
Translational periodicity and symmetry in the fivefold symmetry axes are forbidden in ordinary crystals, while other axes, such as sixfold axes, are allowed. Assume they are the shortest such displacements consider the combinations of two symmetries a and b with the net result c. The length of c is smaller than either a or b by a factor τ = (Square root of√5 + 1)/2, which is known as the golden mean. The new atomic position, outlined with a dotted line does not coincide with a previous atomic position, indicating that the structure does not exhibit translational periodicity. An array of atoms may not simultaneously display fivefold rotational symmetry and translational periodicity, if it did there would be no lower limit to the spacing between atoms.Density functional theory with the jellium model show that clusters with triangular [in two dimensions (2D)] or tetrahedral [in three dimensions (3D)] shapes have a strong shell structure and enhanced stability. The shell closings correspond to the lowest magic numbers of a 2D and 3D harmonic oscillator and at the same time to the number of divalent atoms in close-packed triangles and tetrahedrons. The Molecular dynamics and simulations clusters support the results of the jellium model. Asymptotic numbers of multidimensional partitions of an integer and directed as compact female god that formed dna crypto 64-lattice quantum spirit animals is the obvious explanation for evolution. "J"

[53] Gods First Number
Fifty-three is the 16th prime number. It is also an Eisenstein prime, and a Sophie Germain prime.
The sum of the first 53 primes is 5830, which is divisible by 53, a property shared by few other numbers.
53 written in hexadecimal is 35, that is, the same characters used in the decimal representation, but reversed. Four additional multiples of 53 share this property: 371 = 17316, 5141 = 141516, 99481 = 1849916, and 8520280 = 082025816. Apart from the trivial case of single-digit decimals, no other number has this property.
53 cannot be expressed as the sum of any integer and its base-10 digits, making 53 a self number.
53 is the smallest prime number that does not divide the order of any sporadic group
https://steemit.com/religion/@j1337/the-bible-triangle-prophecy-code-of-gematria-t-numbers
https://steemit.com/spiritual/@j1337/733-337-top-secret-confidential-for-your-eyes-only-73-37