이차방정식과 함수이야기(1)
이차함수와 이차방정식에 대해 써보려 합니다~
(*이 글은 매우 개념적인 내용들을 담고 있습니다.)
교육과정에서 이차방정식은 최초로 중학교 2학년 때 등장해요.
이 시기에 그 유명한 ‘근의 공식’을 배우게 됩니다.
(배운지 몇 년이 지나도 기억한다는 악랄한 공식이죠.)
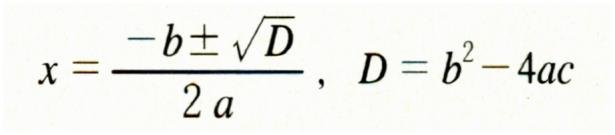
「근의공식 - 출처:네이버 백과사전」
그리고 고등학생이 되면 이차방정식과 이차함수에 대해 다시 배우게 되는데
강렬했던 근의 공식의 인상 때문인지 일부 학생들이 이차함수를 배울 때
이차 방정식과 별개로 보는 경향이 있더라구요.
그래서 그들 사이의 관계에 대해 짤막하게 써보도록 하겠습니다!
우선, 이차방정식의 일반형은 ax^2+bx+c = 0 입니다.
(이차식의 정의에 의해 최고차항의 계수인 a는 0이 아니어야겠죠. (a≠0))
위의 방정식을 참으로 만드는 x값을 근 또는 해라고 부르고
그 근을 구하는 공식이 바로 ‘근의 공식’입니다.
자 그렇다면, 이 근이라는 것은 함수에서 어떤 위치에 존재할까요?
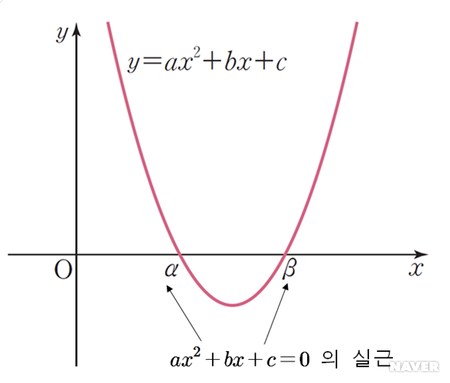
「이차함수 그래프와 근 - 출처: 네이버 백과사전」
위 그림에서 보시다시피, 좌표평면에서 그래프와 x축이 만나는 점(α, β)이 바로 방정식의 ‘근’입니다.
함수가 두 개 이상 그려질 때 우리가 특별히 주목해야 될 점이 있습니다.
바로 그래프끼리 만나는 점인 ‘교점’인데요,
교점은 함수에 대한 문제를 풀 때 우리에게 많은 힌트를 주는 아주 중요한 점이죠.
그 중 x축과 만나는 점에 대해 특별히 방정식에서는 ‘근’이라고 이름을 붙이게 됩니다.
이 x축과의 교점인 ‘근’에 대해 함수적인 해석으로 들어가 보겠습니다.
우선 ax^2+bx+c = 0의 방정식을 두 개의 함수로 나눠보겠습니다.
y = ax^2+bx+c 과 y = 0으로 나눠볼텐데요,
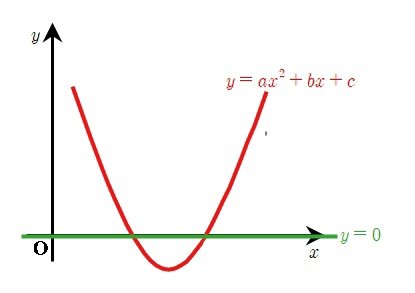
위 그림에서 이차함수를 f(x), y=0을 g(x) 라고 이름 붙인다면 f(x) = g(x) 라는 식이 되겠죠?
f(x) = g(x)라는 식은, ‘두 함수가 같다’라는 단순 기호적 해석이 아닌
함숫값이 같은 x좌표를 찾는 식으로 이용되며
두 함수의 ‘교점’을 찾게 되는 식으로 잘 알려져 있습니다.
여기서 y=0이라는 상수함수는, 좌표평면상에서 x축을 의미하기 때문에
위 식은 f(x)가 x축과 만나는 ‘교점’을 찾아달라는 의미가 됩니다.
즉, ax^2+bx+c = 0의 근을 구하라는 문제는
넓은 의미에서 x축과의 교점을 찾아달라는 문제였던 것이죠!
앞으로 방정식에 대한 문제를 풀게 된다면 사고를 좀 넓혀서
ax^2+bx+c = 0를 읽을 때,
‘함수가 x축과 만나는 지점의 x좌표값을 찾아야 겠다’라고 생각하면
이후 문제해석에서도 큰 도움이 될겁니다 !
첫 글이라 매끄럽지 않을 수도 있지만 차차 다듬어가도록 하겠습니다 !
혹시나 내용에 대한 오류, 오타 등이 있다면 언제든 지적은 환영입니다!
우선 계획은 2,3,4차 함수에 대한 내용을 다뤄보려 합니다.
하지만 이차함수에서 아직 다루지 않은 내용들이 많기 때문에 당분간은 이차함수에 대한 이야기가 이어집니다!
읽어주셔서 감사합니다 :)
Congratulations @ryeons! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
You can view your badges on your Steem Board and compare to others on the Steem Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPVote for @Steemitboard as a witness to get one more award and increased upvotes!