You are viewing a single comment's thread from:
RE: Computation Contest #2 Results and Solution
Do we even know that the zeros of the truncated sum have anything to do with the zeros of the real function? Like say you have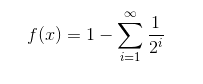
Then f is 0 but all the finite sums have no zeros.
There is an important difference between the sum I chose and the function you show:
Your function won't give a graph where you could read the zeros( by checking for sign changes).
If you have a sum that converges then you can conclude that your graph will be within some small range ε of the graph of the infinite sum. So the zeros you can read in the partial sum graph should also closely match those in the infinite sum graph.