Project // Digital Odyssey - Part 2: Boolean Logic and Gates
Project // Digital Odyssey
From 'Bits' to 'Hello World'... and Beyond.
Chapter 1 - Hardware and Theory
Part 2: Boolean Logic and Gates
As promised in the last part, this time we will have a look at logic gates and how to build components for binary arithmetic utilizing them. Check out the Table of contents for a project introduction.
I have been busy for the last week, designing and testing a working model of a very basic processor unit. You can see the final results of my efforts in figure 1. As I have mentioned in the project introduction, our goal for Chapter 1 will be to build a similar processor from scratch. It's not as complicated as it might seem.
Before we start digging into registers, bit arithmetic and clock cycles though, let me get the fundamentals of Boolean operations and logic gates out of the way. Boolean is a term named after George Boole - an English mathematician and philosopher - and it refers to a domain of mathematics or logics that deals with two valued objects... something we should be quite familiar with after Part 1. Boolean operations accept a certain number of two valued inputs and spit out one or more two valued results - exactly what we need to manipulate our binary encoded numbers. Finally, a logic gate is just a specific implementation of a Boolean operation, be it abstract or as concrete as a circuit board with little MOSFET transistors soldered onto it. The most straight forward gates have only one input and one output. If we consider all possible combinations of states that our in- and outputs can take on, there are four imaginable gates:
1) One that does output a high signal independent of the input (tautology),
2) one that copies the input state to the output (identity),
3) one that outputs the opposite value of the input (negation) and
4) one that emits a low signal independent of the input (contradiction).
These behaviors can be summarized using tables which show all possible inputs and the resulting outputs as displayed in figure 2.
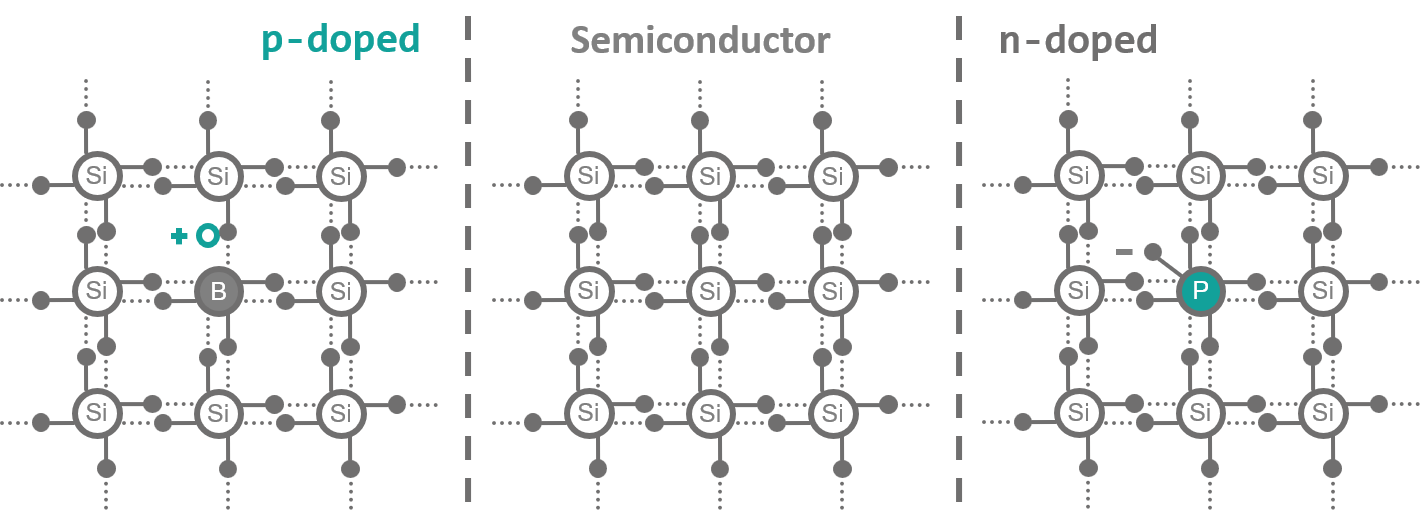
Let's have a little trip into the realm of semiconductors: Say, you want to implement a negation operation with electronic components to build a logic gate. There are different approaches on what components to use. The most common ones are called Transistor-Transistor-Logic (TTL) and Complementary Metal-Oxide-Silicon (CMOS) technology. I will stick to TTL as it is build from good old NPN and PNP Bipolar Junction Transistors (a good introduction to CMOS transistors can be found here [1]). With few words, a transistor is made by sandwiching either a n- between two p-doped semiconductors or vice versa. What's n- and p-doped? Basically, your run-of-the-mill semiconductor atom Silicon (Si) can make up to 4 chemical bonds with other atoms in its surrounding by pairing their outermost (valence) electrons with them. As long as there are only Si atoms present, everyone gets to hold hands with their Si neighbors and all are happily living together. When, however, you introduce trace quantities of a different atom species into the party, things change dramatically. Commonly, Phosphorus (P) is used for n-type semiconductors. As P atoms have 5 valence electrons to bond with, when they are introduced to the Si lattice, only four of them can be paired. The fifth electron stays unpaired and is available as a negative charge carrier (n-type for negative). Boron (B) on the other side has only 3 valence electrons and therefore leaves an electron 'hole' in the Si lattice when mixed in. This absence of a negative charge acts like a positive charge carrier (hence, the material is called p-type). Have a look at figure 3.
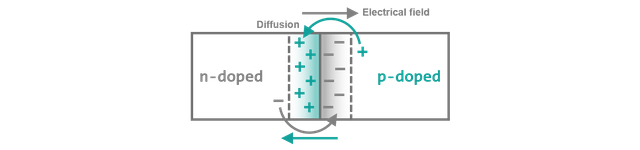
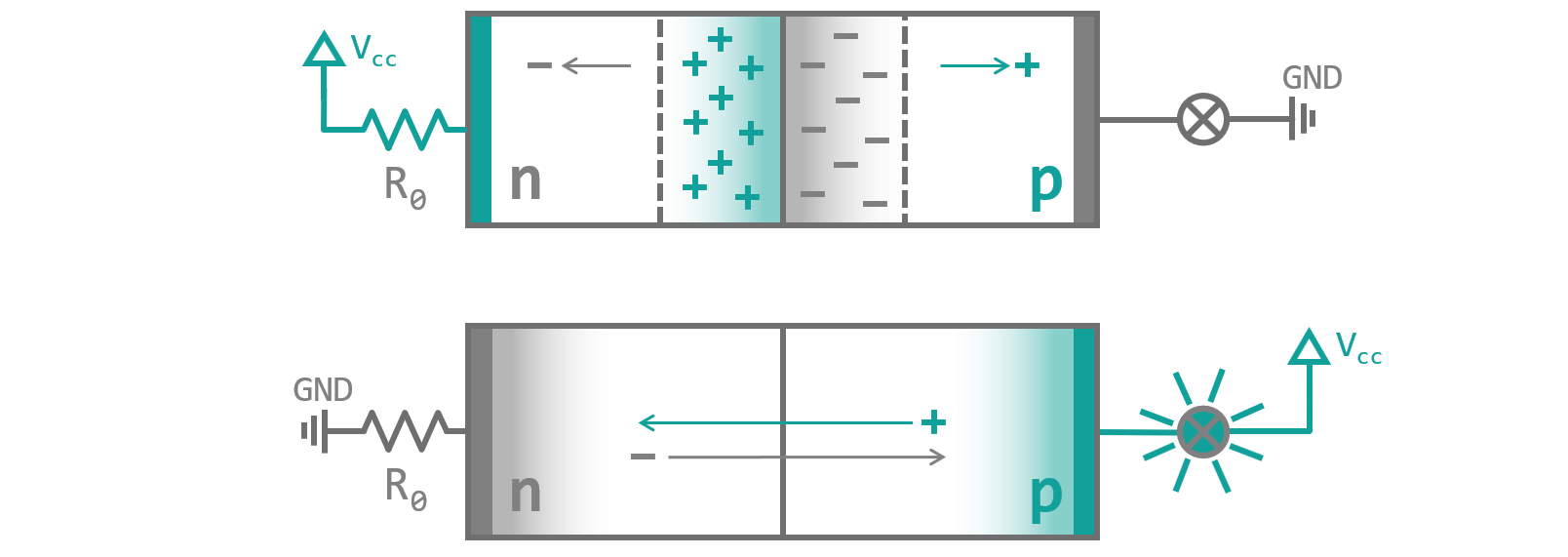
The magic happens when you combine both types. As you deposit a n-type semiconductor onto a p-type, because of the attractive force between positive and negative charges, holes and electrons from the two adjacent layers start to recombine with each other (diffusion process). Concurrently as the charge carriers are neutralized, they are missing from their source layers and therefore, the once neutral materials start developing opposite charges, creating an electrical field. The electrical fields acts upon the electrons and holes and create counter forces drawing the charge carriers back. At some point a state of equilibrium is reached between this force and the original force driving the recombination, so everything comes to a halt. Therefore, not all charge carriers are used up in the process but only a small strip between the layers becomes neutral (the so-called space charge region). Figure 4 shows this process schematically.
When you apply a voltage from n- to p-type semiconductor, depending on where you put your + and - poles, different observations can be made: When + (more generally called supply voltage (Vcc)) is connected to the n-type and - (called ground (GND)) to the p-type layer, electrons and holes are drawn away from the neutral zone between the layers and its size increases. As no charge carriers can pass between the p-n-junction no current is flowing. If you change polarity, charge carriers are pushed into the neutralized zone, depleting it. As soon as your voltage is high enough, the space charge region can be overcome and charge carriers begin to travel between the layers again... a current is flowing. Congratulations, you have just discovered the diode - an electrical component that is only conductive in one direction of current flow (see fig. 5).
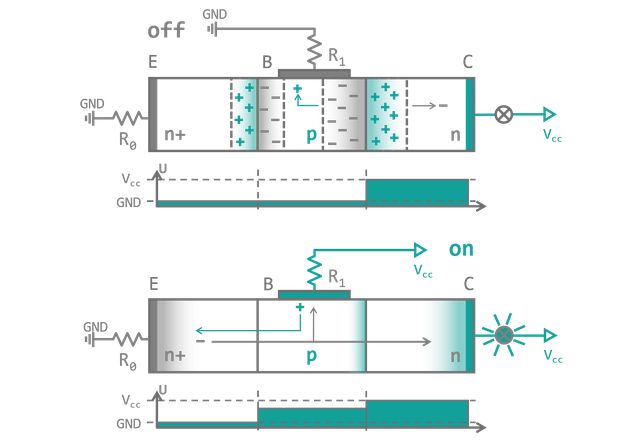
Now we add a third doped semiconductor layer to our setup in a way that results in an alternating pattern like n-p-n. The second n-type layer has to be more strongly doped (denoted by n+) to give it a surplus of electrons compared to the number of holes present in the p-layer. When a voltage source is connected, GND at n+ (called emitter (E) in the following) and Vcc at n (the collector (C)), nothing really happens. The transistor basically looks like two diodes facing in opposite direction, so no current can pass either way. "Cool, why not cut the wire instead? Same effect, less effort, right?". Patience! There is a third connection available on the p-type layer - the so-called base (B). Depending on its potential difference to the other connections different modes of operation are possible. The relevant ones for us are summarized in figure 6 (a more detailled description of all transistor operation modes can be found in [2]). When the base connection is pulled to ground potential, the barrier between B and C increases and no current can pass from C to E. On the other hand, if B is pulled to Vcc, the space charge region between B and E vanishes and electrons and holes can pass between the connections leading to a small current flow. Since the n+ layer has more free electrons than holes are available from the base, not all electron coming from the emitter will recombine. The base is designed to be small enough that the surplus of electrons can easily diffuse through the layer and are pushed through the space charge region between B and C. They are then attracted by the positive potential at the collector and leave the transistor, ultimately leading to a high current flow between C and E.
TLDR; a transistor can behave like a switch that is controlled by an electrical signal.
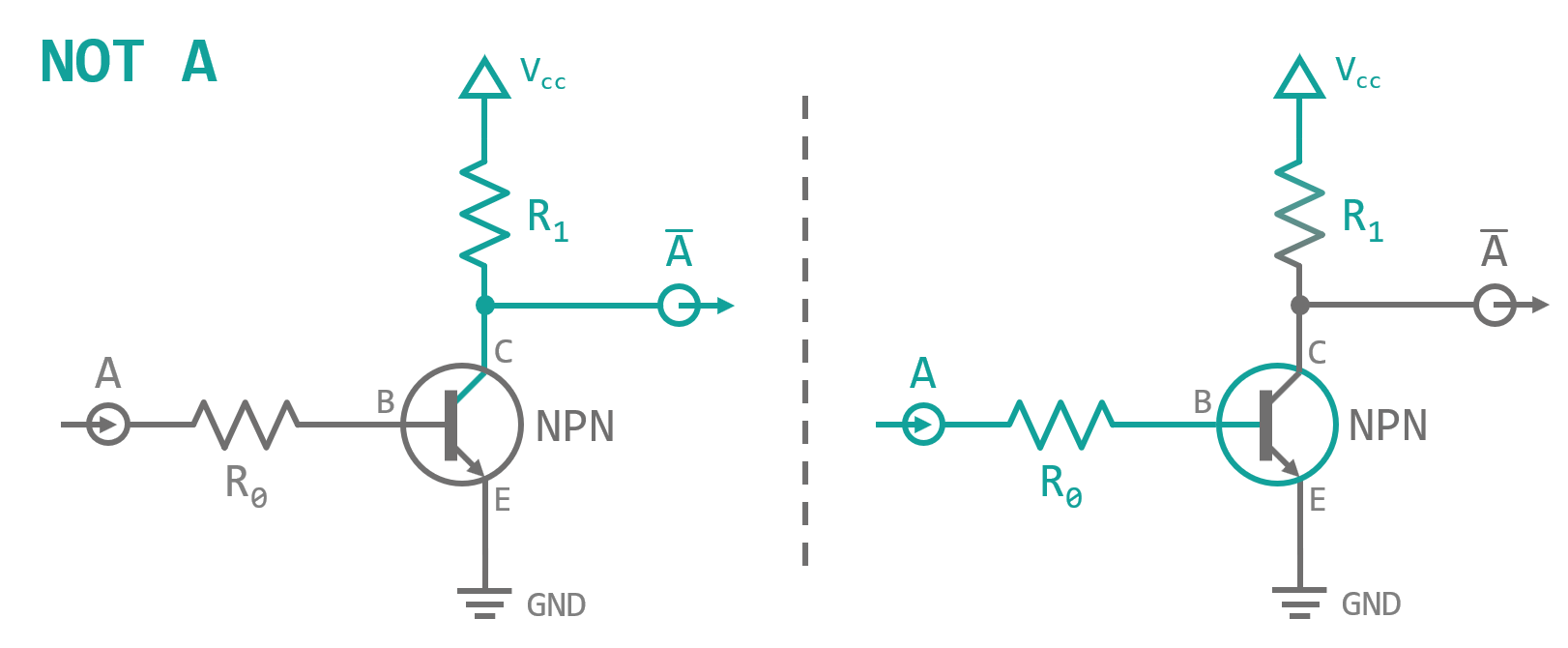
Finally, we can return to our original problem: Building a negation operation using transistor logic. This so-called NOT gate is quite easy to implement and uses only one transistor. When our incoming signal is low (that means pulled to GND) we want our outgoing signal to be high (pulled to Vcc). This is achived by connecting our output to Vcc via a resistor (R1) and the collector of a NPN transistor. The transistors base is connected to the input and its emitter is directly contacted to GND. See figure 7 for a schematic view. While the input is pulled to ground, no current flows between E and C of the transistor, so the output stays pulled to Vcc. When the input is high, the transistor switches on and a current can flow between Vcc and GND effectively pulling the output to GND. The resistor R1 is very important as it serves two purposes here: 1) If no resistor was used, the switching transistor would short out GND and Vcc which leads to a high current flow that could potentially fry the transistor to a small ugly blob of charred silicon. 2) By using a resistor between output and Vcc, we are making sure that our output is definitely on GND potential after the transistor switches. Otherwise the output was connected to Vcc and GND at the same time and (at least in theory) with equal resistance on both paths. Instead of having a defined state after being switched on the results would be a value somewhere in between high and low, potentially flipping the next input on or off without our blessings - an undefined state.
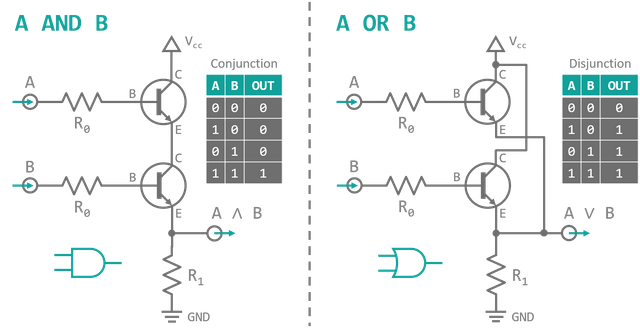
Last but not least, I want to introduce two more basic Boolean operations and their gates (shown in fig. 8). First is the AND gate which takes in two inputs and will output a high signal only if both inputs are high at the same time. This is implemented by connecting two NPN transistors in series. A current will only flow, pulling the output to Vcc, when both of their bases are activated. The second one is the OR gate which also takes in two inputs. It puts out a high signal, if any of the inputs are in a high state. This can be achived by connecting two transistors in parallel. A current will flow from Vcc to output if any of the transistors is conducting. Together with the NOT gate they will serve as building blocks for more complex components. In theory there are 16 different gates with 2 inputs and 1 output (2 output values for each of the 2·2 possible inputs). However, you only need a choice few of them, since all other parts can be made by clever combinations of specific subsets (check out [3] for more information). Even AND, OR and NOT could be reduced further since AND and OR might be expressed using NOT and the other alone:
A OR B = NOT ((NOT A) AND (NOT B))
You can check it for yourself. In practical application you try to reduce the number of different gates used, as it is easier to manufacture the same part a lot of times instead of many different parts in smaller numbers. However, I do not plan on selling my processor, so in order to keep the complexity as low as possible I will not break every logic gate down into ORs and NOTs.
In the next part I will show you how to combine our shiny new logic gates into larger functional groups and build our first processor components. Stay tuned.
[1] Electronic Tutorials, The MOSFET (web)
[2] Transistor Basics (pdf)
[3] Functional Completeness (web)

Ah...how logic is in every aspect of reality.
Very true indeed. It really helps to understand the fundamentals of Boolean algebra and logic. The rules that apply to simple True or False statements in mathematics easily translate to everyday life problems.