Computation Contest #5 Results and Solution
Solution
The problem of this contest was to solve the exponential integral numerically using taylor series from 0.9 to 1.1:
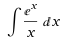
First of all I want to apologize for telling you to solve a problem with a method that cannot be used to solve it, but learning by mistakes is always the best way to learn.
And now, here is my code:
public class TaylorIntegration {
// x!
static double faculty(int x) {
double res = 1;
for(int i = 2; i <= x; i++) {
res *= i;
}
return res;
}
// Generates the ferst terms of the taylor polynomial of e^x at x.
static double[] generateTaylorExp(int terms, double x) {
double[] coefficients = new double[terms];
double y = Math.exp(x);
for(int i = 0; i < terms; i++) {
coefficients[i] = y/faculty(i);
}
return coefficients;
}
// Generates the first terms of the taylor polynomial of a power function.
static double[] generateTaylorPower(double coef, int power, int terms, double x) {
double[] coefficients = new double[terms];
for(int i = 0; i < terms; i++) {
// Generate the coefficient:
coefficients[i] = coef*Math.pow(x, power)/faculty(i);
// Differentiate the function:
coef *= power;
power--;
}
return coefficients;
}
public static void main(String[] args) {
int size = Integer.parseInt(args[0]); // Generate the taylor polynomial with 100 terms
double x = 1;
double[] taylorExp = generateTaylorExp(size+1, x); // Generate one additional term to compensate from the loss when divided by x.
double c1 = taylorExp[0]; // Coefficient in front of the 1/x term after dividing by x.
double [] taylorx = generateTaylorPower(c1, -1, size, x); // Generate a polynomial to approximate 1/x at x = 1;
// Create the total taylor polynomial by summing up the parts:
double [] taylor = new double[size];
for(int i = 0; i < size; i++) {
taylor[i] = taylorx[i]+taylorExp[i+1]; // Remember that exp is divided by x, so the actual powers are 1 less then the index.
}
// Integrate:
double[] integrated = new double[size+1]; // By integration the number of terms is increased, because of "+C"
for(int i = 0; i < size; i++) {
// Perform integraion using the power rule:
int newPow = i+1;
double newCoef = taylor[i]/(newPow);
integrated[i+1] = newCoef;
}
// Caclulate the integral you want:
double x1 = 0.9, x2 = 1.1;
double res = 0;
for(int i = 0; i <= size; i++) {
res += (Math.pow(x2, i) - Math.pow(x1, i))*integrated[i];
}
System.out.println(res);
}
}
And that gives the following results depending on the number of terms in the taylor expansion:
99 → 180.5206161521858
100 → -194.07526420957734
101 → 213.90044721848423
As you can see, it's a mess…
Why is that?
The problem lies in the function 1/x.
At x = 1 it's coefficients are always ±1. So if one adds higher terms they won't be reduced by some n! like with e^x and so they will get really high for the upper border of the integral since 1.1^x grows to infinity. Because of the ±1 term the result changes between positive and negative.
Even when trying to integrate other points of this function the method it fails. Again because the derivatives of 1/x kill the 1/n! terms in the construction of the taylor series.
Is the whole method wrong then?
No!
The method is actually pretty good and most importantly it can be far more exact for small values of (x₂-x₁) than normal numerical integration.
The method is just not applicable for every function at every interval.
I hope you learned as much reading this as I did when programming this.
I think I will also make the next contest about this topic(Unless you protest).
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
List of participants with their entries:
| Name | Solution found | Comment |
|---|---|---|
| @kaeserotor | NONE, problems modelling taylor series | I don't exactly know what problems you had, but maybe you discovered exactly what you where supposed to do, but then thought you did a mistake. Anyways because you are the only person who tried you will get the reward! |
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
Winners:
Congratulations @kaeserotor, you won 2 SBI for trying to solve it!
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
Thanks a lot, I don't feel like I deserve any reward but thanks anyway :D
Also, I learned a lot trying this and even more through your explanation. Thank you!