Word-search algorithms, part 3: precomputation and intersection
The algorithms presented in part 1 and part 2 used data structures to let us answer questions of the sort "what words contain these given letters, plus some extra?" or "what are smaller words composed of a subset of these letters?" Both created data structures that were only a small multiple of the original size of the dictionary.
When the total dictionary is only 2.6MB in size (267,751 words), we can afford to throw a lot more memory at the problem, and this can speed up searches.
Precomputation
Suppose we want to input K letters and get all words containing those letters. That means there are less than 26^K possible inputs. In fact, since order doesn't matter, it's the multiset number ((26,K)) = (K + 25 choose 26).
We can easily precompute the results and store them (as 19-bit or 32-bit indexes into the original dictionary list, for compactness.) The question is, how many such precomputed indices can we afford to store? Here's some Python code to explore the index size:
def computeIndexSize( k ):
indexSize = {}
for w in allWords:
signatures = set( "".join( c )
for c in itertools.combinations( sorted( w ), k ) )
for s in signatures:
indexSize[s] = indexSize.get( s, 0 ) + 1
print len( indexSize ), "indexes of size", k
totalSize = sum( z for z in indexSize.itervalues() )
print totalSize, "total entries in indexes"
largest = max( (v,k) for (k,v) in indexSize.iteritems() )
print "Largest index:", largest
smallest = min( (v,k) for (k,v) in indexSize.iteritems() )
print "Smallest index:", smallest
return indexSize
For the table below I've computed the size using 32 bits per entry.
| K | number of indexes needed | total index entries | index memory usage | largest index | smallest index |
|---|---|---|---|---|---|
| 2 | 351 | 6,989,965 | 26.7 MiB | 'ES', 117058 | 'JQ', 19 |
| 3 | 3,217 | 16,382,683 | 62.5 MiB | 'EIS', 69656 | 'DXX', 1 |
| 4 | 21,154 | 28,262,608 | 107.9 MiB | 'EIRS', 37973 | 'ADFJ', 1 |
| 5 | 100,513 | 38,200,922 | 145.8 MiB | 'EIRST', 20779 | 'AAAJZ', 1 |
| 6 | 349,978 | 41,969,858 | 160.2 MiB | 'AEIRST', 11179 | 'AAAACW', 1 |
| 7 | 903,604 | 38,291,264 | 146.1 MiB | 'AEINRST', 6086 | 'AAAAACG', 1 |
| 8 | 1,742,243 | 29,310,606 | 111.8 MiB | 'AEINORST', 3093 | 'AAAAAASS', 1 |
Even combined, all of these sizes are totally reasonable to keep in memory. At K=7, the mean index contains just 42 entries, so we're probably close to the point of diminishing returns. At K=8 the index of indexes is now a significant portion of the overall data structure.
Fast Intersection
We can augment a set of precomputed tables using intersection to serve larger queries than what we have precomputed. For example, if we want to look up words containing "EJQS", we could look at the list for "ES" and the list for "JQ" and compute their intersection for words that contained all four letters.
Why not simply take the smaller of the two tables and scan it for the desired letters? (Or, convert the index into a suffix tree that permits the query?) These are reasonable ideas, and may work best in practice. However, in some cases it is possible to do the intersection in less time than doing a complete scan! The best procedure may actually be to switch between intersection and scanning one of the indicies depending on the actual sizes, or even switch algorithms based on how long our "first choice" is taking.
Additionally I think fast intersection is neat and wanted to talk about it. :)
There are two parts to such a design: a query planner and an intersection algorithm. The query planner should look for indexes that make the intersection step faster, which can be itself a nontrivial problem! But "good enough and fast" is probably our design goal.
If we have an 8-letter input and look at all the 8C4 = 70 ways to split it into equal pieces, that is a reasonable amount of planning work. But 12C6 = 924, which seems like a scarier number before we even get any real work done. A fast heuristic is to sort the input letters by overall frequency, which should result in one "big" bucket and one "small" bucket. This is advantageous whether we're doing an intersection test, or just scanning the small bucket.
Intersection on sorted sets
The paper by Baeza-Yates and Salinger (2010) referenced below gives an overview of some algorithms and introduces a new one with good average-case performance. The key idea is to do binary search on the two sets, instead of comparing all of their elements.
If we simply merged the two sorted lists element by element (throwing out words that appeared only once), we would perform ϴ( m + n ) comparisons. That's not bad, but when n is much larger than m it's not good, either, and it is expensive even in cases where there are no intersections. The same applies to building a hash table from one list and and then checking all of the elements of the other list. (However, I should note that in the context described above, we should be able to have the hash table all ready to go in memory.)
If Q (of size m) is a small set and D (of size n) is a large set, then we can do better by performing binary search on D for every element of m. That gives us time that's O( m log n ), much better. We may also be able to abort our search if we run out of elements of D, since each search can start where the last one left off (because Q is also sorted.)
A somewhat more complicated algorithm from [Hwang 1972] called "binary merge" achieves O( m log (n/m) ).
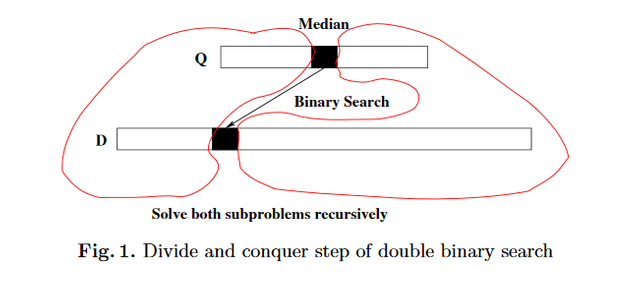
Baeza-Yates and Salinger's algorithm is based on a divide-and-conquer approach sketched in this figure from their paper:
Start with m, the middle element of Q. Binary search for it in D. When we've found either a match, or the place where a match would be, then that gives us two smaller sub-problems:
- the elements of
Qless thanmmust all be in the left portion ofD(elements less thanm) - the elements of
Qgreater thanmmust all be in the right portion ofD
So, we can recursively search each of the two subproblems, switching Q and D around if the sizes of the subproblems reverse.
They show this algorithm has worst case O( m log n ) when m is small compared to n. The number of comparisons in this worst case are better than binary merge when n/m is greater than about 6.3. The authors also compute an average-case analysis and calculate that their algorithm has a lower constant factor than binary merge, as well as providing some simulation results.
Conclusion
Computer are growing in capability much faster than the English language. The fastest choice for some word-search problems may simply be to precompute a large enough fraction of the possible queries, which requires an amount of memory that is completely feasible. (Spilling to a flash device is also plausible and would not affect end-user observed response times by very much.)
It is also possible to efficiently compute the intersection of two or more precomputed word lists, but it seems like the best technique will probably be a hybrid depending on the relative lengths of the lists. Such a hybrid model will depend to a great extent on the efficiency of the actual implementation, rather than purely theoretical concerns.
Further Reading
Word-search algorithms: part 1, signatures and hashing
Word-search algorithms: part 2, tries
Baeza-Yates, Ricardo & Salinger, Alejandro. (2010). Fast Intersection Algorithms for Sorted Sequences. "Algorithms and Applications, Essays Dedicated to Esko Ukkonen on the Occasion of His 60th Birthday", pp. 45-61. doi:10.1007/978-3-642-12476-1_3. (P.S. It's the same Ukkonen who developed a linear-time suffix tree creation algorithm!)
Hwang, F.K., Lin, S. (1972). "A Simple algorithm for merging two disjoint linearly ordered lists". SIAM J. on Computing 1, 31–39
Hello! Your post has been resteemed and upvoted by @ilovecoding because we love coding! Keep up good work! Consider upvoting this comment to support the @ilovecoding and increase your future rewards! ^_^ Steem On!

Reply !stop to disable the comment. Thanks!