A "trie" is a data structure useful for string operations. It's also called a prefix tree, or sometimes a radix tree. I prefer to pronounce it as "try" to distinguish it, but the etymology of the word comes from "retrieval", and the person who coined the term pronounces it "tree".

In the previous article I talked about we could convert strings to signatures and use a hash table to identify anagrams or sub-words. A trie can be used in the same way, and more.

Trie structure

A Trie is a directed tree structure with nodes connected by edges, starting from a root node. But each internal node may have multiple outgoing edges, and each such edge is labelled with a different label--- for word problems we'll use individual letters as our labels.

The trie invariant is that the set of labels on the path from a root to a leaf node, form a prefix of the key stored in that leaf. So, if we want to store 'AERT' in a trie, the path from the root to its storage location might look like this:

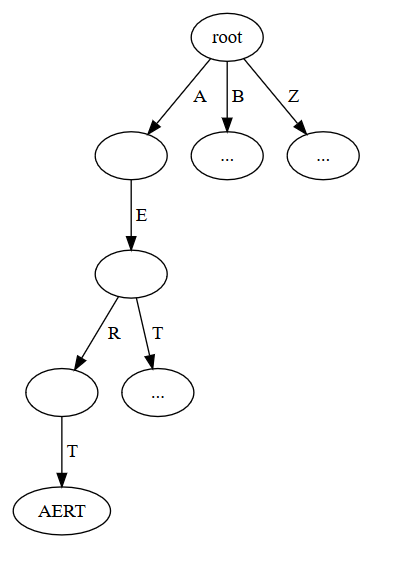
(Figure generated with graphviz.)

There are different variations in use. Generally it is permissible to have an incomplete path if a key has a unique prefix. Some implementation use a special end-of-string symbol (like $) to differentiate a lookup of say, ALGORITHM from ALGORITHMS. The parent node of ALGORITHM would have at least two children, one labelled with S and the other with $:

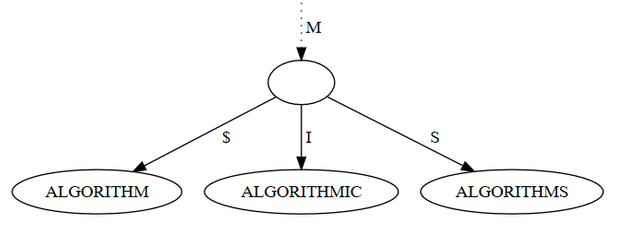
Other implementations just allow any node to store a key, even if it has children, so that ALGORITHMS would be stored in a child node of ALGORITHM.

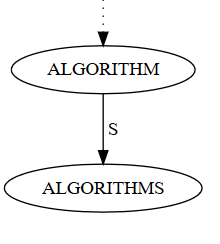
The Wikipedia article gives an example Python implementation that uses this latter convention, which is more natural. However, the end-of-string convention is used when creating suffix trees, as explained below.

To look up a key in a trie, simply follow the edges corresponding to the letters in that key, one by one, until we hit a leaf node, or there is no corresponding edge.

Prefix matching with tries

Start at the root. Then all of the words starting with "A" are in the subtree labelled "A". All the words starting with "AB" are in the subtree labelled "A" and then "B", etc. So if we want a list of all words starting with a given prefix, the trie gives us an easy way to enumerate them. (In this case, the trie should be populated with the ordinary versions of the words, not their signatures!)

A trie could be populated in reverse order if we wanted to do suffix matching.

Anagrams and tries

A trie could be used as a replacement for the hash table use in the previous article, to store the signature for each word, where the signature is the sorted letters.

This gives us a little bit more extra structure. The subtree starting with "A" contains all words containing an A, the subtree starting with "B" contains all words containing a B (but not an A), etc. This is not quite what we'd like for most purposes. Suppose we want to find words containing "JA". The subtree A, J contains some of these words, but not all--- it omits words that contain a B, C, D, E, F, G, H, or I. Those live in the subtrees A, B or A, C, etc.

We could develop a search algorithm which looked in each of the subtrees that has not already been ruled out. For example, if we are looking for "JA" words, then we never have to visit a subtree with label K or greater. But this would not be very efficient. The right data structure is an elaboration of the trie called a suffix tree.

Suffix trees

The efficient construction of this data structure can get pretty mind-bending (and it can be done in only linear time!) but let's just ignore that for now and focus on what it does and how to use it.

Logically, a suffix tree is a trie containing all suffixes of a given string. So if our string is "SUBSTRING", the suffix tree is a trie with keys"G", "NG", "ING", "RING", "TRING", "STRING", "BSTRING", "UBSTRING", and "SUBSTRING".

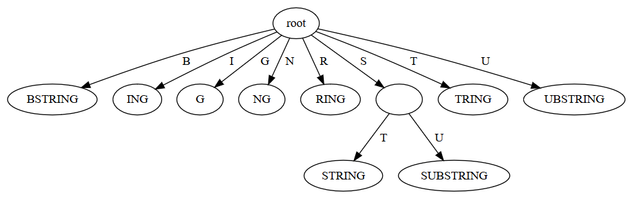
Substring search

One way this is useful is if we want to say "does string X contain string Y?" If we have the suffix tree for string X, then we can just look up string Y using the trie lookup procedure. So, does "SUBSTRING" contain "STRING"? Yes, because we search root -> S -> T in the trie, and there it is.

This algorithm can with only a little effort gives us all the locations at which the substring occurs. If we want all places where "THIS" occurs, they are all and every leaf under the path root -> T -> H -> I -> S. Walking that subtree will return all suffixes that start with THIS; each suffix identifies the location of THIS in the original string.

Suffix trees on dictionaries and glob search

To use a suffix tree on a dictionary, we create one enormous string containing the entire dictionary, with special separators between each word:

"$AA$AAH$AAHED$AAHING$AAHS$AAL$AALII$AALIIS$AALS$AARDVARK$AARDVARKS$AARDWOLF$AARDWOLVES$AARGH$AARRGH$AARRGHH$AARTI$AARTIS$AAS$AASVOGEL..."

and create the suffix tree for this string. How does this help us? Well, suppose we want to find all words that start with A and end with K.

Using the algorithm explained above, we can easily find all locations where "$A" occurs: an A at the start of a word. We can also search for "K$" and find all the locations where there is a K at the end of a word. Then we can match the two lists to see if two instances correspond to the same word or not. Only the $A closest to the $K position is a valid candidate.

In the dictionary above: "K$" matches at position 55. "$A" matches at position 0, 3, 7, 13, 20, 25, 29, 35, 42, 47, 56, ... The one closest to "K$" is 47, so we check positions 47-55 and verify that it's a single word, AARDVARK.

The same idea can be used to efficiently search for any pattern of wildcards. For example, searching for A*V*K requires us to search for "$A", "V", and "$K" and look at the cases where a V occurs between the other two. More wildcards just means more indexes to track.

Suffix trees and acronyms

This technique can be used to search word signatures instead of words. If we are interested in any word we can make with Q, C, P and D, then:

1. Create a suffix tree from the list of all word signatures (the sorted versions of their letters.)
2. Sort the desired letters into alphabetical order and insert wildcards between non-adjacent letters to get *CD*PQ*
3. Search the suffix tree for *CD*PQ* in the manner described in the previous section, by finding all occurrence of CD and matching them with occurrences of PQ

As promised, this techniques overcomes the scaling limitations of hash lookup. We don't have to guess what letters might be added to CDPQ to create a word, or try all the possibilities. Instead, the suffix tree efficiently points at signatures that contain CD, and signatures that contain PQ, and we simply filter to those that have both, like "ACDEEEINNOPQRU" (EQUIPONDERANCE).

The computational cost here is that we do have to process each match; so if we search for "E" then that is going to be quite a lot of hits to wade through. But it's never going to be more than the number of letters in our dictionary.

Constructing suffix trees efficiently

A suffix tree has as many leaves as the input length. There's one suffix of length N, another suffix of length N-1, etc. But we want to avoid storing O(N^2) characters in the tree. We can "compress" the tree by storing suffixes as a position and length in the original string, not by a copy of the characters.

This means all those very long but unique suffixes like "AH$AAHED$AAHING$AAHS$AAL$AALII$AALIIS..." can be represented by just a pair of numbers. The previous example with "SUBSTRING" would look something like this:

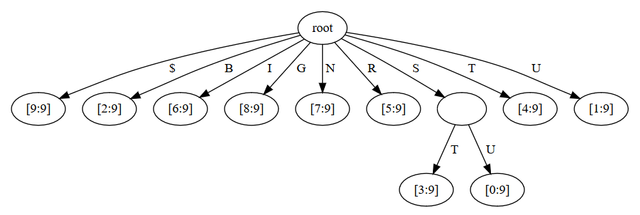
We also have to use a different separator between each word in the dictionary, in order to prevent any suffix from being a substring of another suffix. For example, we don't want a "ZZ$" at the end of our dictionary to be considered a substring of "BUZZ$"; this would mess up our tree structure.

Once we make these adjustments, there are several linear-time algorithms for suffix tree construction which I won't get into here, but can be found in the references below.

Conclusion

Equipped with a suffix tree, we can now search for any letters we must use in a word game, and get any words containing those letters, plus some extra ones. This list can be filtered further if there are letters we should avoid, as a post-processing step. The algorithm has no more problem returning 14-letter words than 5-letter ones.

This is a clear win if we have, for example, four letters and want to find an eight-letter word that uses all of them. It's less obviously a win for searching for shorter words that we can make, but the algorithm sketched above for wildcard search can be adopted to list words that match any one of the search letters instead of all of them.

Further Reading

Part 1: Signatures and Hashing

McCreight, Edward Meyers (1976). "A Space-Economical Suffix Tree Construction Algorithm". Journal of the ACM. 23 (2): 262–272.

Ukkonen, E. (1995). "On-line construction of suffix trees". Algorithmica. 14 (3): 249–260.

Wikipedia, Suffix Tree.

Wikipedia, Trie.