Summing Factorials in F* With Dependent Types

markgritter (59)in #programming • 3 years ago

A beginning programming challenge is: write a program that sums all the factorials between 1! and N!, where N is given as input.

Let's make that into a much harder programming challenge by writing a program that contains a proof that our algorithm works! The language I'm learning now is F*, pronounced "F-star". F* has "dependent types", which will allow us to specify properties about our program in that program's types. You can follow along using the F* interactive editor.

What's a factorial, anyway?

Let’s define factorials and a sum function so we can tell what the algorithm is supposed to do. Strangely, “sum” does not seem to be part of FStar’s standard library, even though it has a bunch of stuff about the Euclidean algorithm and a lot of lemmas.

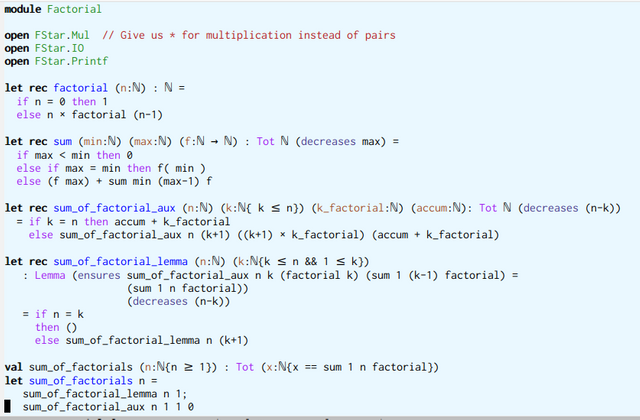
module Factorial 
 
open FStar.Mul // this lets us use * for multiplication
// otherwise it represents a type product
 
let rec factorial (n:nat) : nat = 
  if n = 0 then 1 
  else n * factorial (n-1) 
 
let rec sum (min:nat) (max:nat) (f:nat -> nat) 
: Tot nat (decreases max) = 
  if max < min then 0 
  else if max = min then f( min ) 
  else (f max) + sum min (max-1) f

Pretty standard recursive definitions here. I had to do a little work with sum; F* requires that any total function (marked by Tot) always terminates. We prove that it does by identifying something that decreases each time. F* tries the argument in lexicographic order if you don’t specify, which is why the factorial function works— I’ll show another example in a minute showing the “something” could be an expression as well as an argument.

F* syntax is very similar to Ocaml, which is good because it's very poorly documented. If you don't know how to do something in F*, look up an Ocaml tutorial instead. :) nat means a natural number. let rec defines a recursive definition, one that is allowed to use itself. Function application looks like f x or (f x).

F* is also doing something under the hood to prove that max-1 is a natural number. What if max is 0? After all, -1 is not a natural number— but then one of the first two cases must hold. F* farms out this logic to a SMT solver under the hood, which is smart enough to tell that if we reach the third case, subtraction by 1 must always produce another natural number, so our function type-checks.

Writing what we mean

Now we can write the type of the algorithm we want. The types followed by {}s are refinement types, specifying extra conditions. For example, we don’t know what 1!+2!+3!+…+N! means when N is 0, so we forbid that by requiring a natural number that’s at least 1. And, we say that the result of our function should be the same as (factorial 1) + (factorial 2) + … + (factorial n). We could compute it that way, but that would be inefficient.

val sum_of_factorials (n:nat{n >= 1}) 
  : Tot (x:nat{x == sum 1 n factorial})

Our algorithm

So let’s write a helper function to compute that sum (tail-)recursively, simultaneously building the sum and the factorial:

let rec sum_of_factorial_aux (n:nat) (k:nat{k <= n}) 
 (k_factorial:nat) (accum:nat): Tot nat (decreases (n-k)) 
  = if k = n then accum + k_factorial 
    else sum_of_factorial_aux n (k+1) 
       ((k+1) * k_factorial) (accum + k_factorial)

Here, k is the number we’re currently summing. k_factorial is its factorial. accum is the sum of the factorials so far, and n is our upper bound.

We again have to prove to F* that our function terminates. We identify the value that decreases: the difference between n and k, which eventually reaches zero.

Can we put it all together?

let sum_of_factorials n = 
   sum_of_factorial_aux n 1 1 0

Nope, this doesn’t type-check. F* is smart, but not smart enough to prove that our algorithm works without some help. We get:

(Error 19) Subtyping check failed; expected type x: nat{x == sum 1 n factorial}; got type nat; Try with --query_stats to get more details

nat is the type we put for our return value of the auxiliary function, not nat with the extra conditions. Sometimes, F* can reason that the extra conditions always hold, but not here. So we could go back and add some more refinement types, but let’s try proving what we need as a lemma.

Writing a lemma

An F* lemma is “really” a function, but one that doesn’t produce any output. It just guarantees some type exists (like an equality.)

let sum_of_factorial_lemma 
   (n:nat) (k:nat{k <= n && 1 <= k}) 
   : Lemma (ensures sum_of_factorial_aux 
                     n k (factorial k) (sum 1 (k-1) factorial) = 
                    (sum 1 n factorial)) 
     =admit()

Our lemma says that if we give the function n, k, k!, and 1! + 2! + 3! + ... + (k-1)!, as inputs, then we get 1! + 2! + 3! + ... + n! as the result. We can just put in admit() for now, which says “trust us, it’s true” and ask F*: if we prove this lemma, will our function type-check?

val sum_of_factorials (n:nat{n >= 1}) 
 : Tot (x:nat{x == sum 1 n factorial}) 
let sum_of_factorials n = 
   sum_of_factorial_lemma n 1; 
   sum_of_factorial_aux n 1 1 0

F* says yes! So let’s prove the lemma, inductively.

I’m leaving out some steps where I messed up and F* said “no“ because I’d gotten the lemma or the starting conditions wrong! For example, sum_of_factorial_aux n 1 1 1 is wrong.

We can write a base case first, and F* is smart enough to verify it’s true. () is the “unit” value. In this context, it means “the lemma is true, prove it yourself.”

let rec sum_of_factorial_lemma 
   (n:nat) (k:nat{k <= n && 1 <= k}) 
   : Lemma (ensures sum_of_factorial_aux 
                    n k (factorial k) (sum 1 (k-1) factorial) = 
                    (sum 1 n factorial)) 
   = if n = k 
     then () 
     else admit()

Operating step-by-step in this way makes it easier to tell if we've gone wrong. If F* can't prove our base case, maybe the lemma is incorrectly stated, or maybe it's too complicated and needs to be simplified further.

Now, what do we need to prove that the lemma is true for a lower k? Well, our equality is true for k = 1 if it’s true for k = 2, if it’s true for k = 3, etc., We’re doing backwards induction. Because it’s backwards, we need to assure F* that the proof terminates, just like we did with the “aux” function itself:

let rec sum_of_factorial_lemma 
   (n:nat) (k:nat{k <= n && 1 <= k}) 
   : Lemma (ensures sum_of_factorial_aux 
                     n k (factorial k) (sum 1 (k-1) factorial) = 
                    (sum 1 n factorial)) 
                    (decreases (n-k)) 
   = if n = k 
     then () 
     else sum_of_factorial_lemma n (k+1)

We don’t actually need to do the algebra, we just pointed out how the proof had to work, and F* took care of the rest. (This time, anyway. Other times we might need to write more lemmas, or use “tactics” to write lemmas for us.)

Finishing up

The last part is to do some I/O, so we can actually use our function. If you've been using the interactive editor you'll notice that F* doesn't actually evaluate anything, it just checks types! You can't call (factorial 15) and see the result. For that we need to export the F* program to another language.

F*'s capabilities are pretty limited, but it does have formatted printing as part of the standard library.

open FStar.IO 
open FStar.Printf 
 
let _ =  
   let n = input_int() in 
     if n >= 1 then 
       print_string (sprintf "%d\n" (sum_of_factorials n)) 
     else 
       print_string "Bad input\n"

Note that the program won’t compile if we don’t put in the bounds check! Because we explicitly said, in its type, that our function only works for n >= 1..

To actually run the program, we get F* to output it as OCaml. (It supposedly does F# as well, but the Wiki says that’s broken, so YMMV.)

fstar.exe  --odir out --codegen OCaml --extract 'Factorial' Factorial.fst --record_hints 
Extracted module Factorial 
Factorial.fst(33,0-38,33): (Warning 272) Top-level let-bindings must be total; this term may have effects 
Verified module: Factorial 
All verification conditions discharged successfully 
ocamlfind opt -package fstarlib -linkpkg -g  out/Factorial.ml -o out/Factorial 
./out/Factorial 
115 
295075440239926806356337310811631807344070986921118635622379820423639769627087910615894907135438362233850988681066258334127135685473542296714148908162189836562063052556442336528920420940313

All done!

Conclusion

We not only wrote an efficient algorithm for the factorial sum, but the program itself contains a proof that it's equivalent to the inefficient version! The F* system is responsible for verifying that the assertions we made-- expressed in terms of types-- actually hold. So we can be confident that, to the extent we specified our original definitions correctly, our code obeys the properties we said it should have. This is a very powerful tool for building reliable software, and F* has been used to create provably correct cryptographic code.

Complete code is available at https://gist.github.com/mgritter/462d81d678609423b0059b632f76c528