Hello my friends! I didn't upload any Java Code for a long time now, but I had in mind to implement Graphs in Java one day and so here we are! We will today talk about the basic Graph Theory you need to understand what a Graph is etc. and also implement a Basic Graph in Java that we will expend upon to do Graph Algorithm Implementation in posts later on! So, without further do let's get started!

Graph Theory:

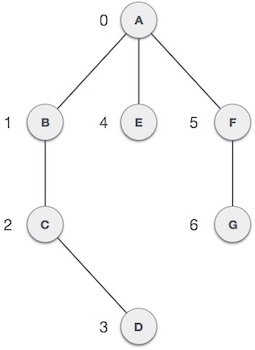
    A Graph is a Datastructure like all the others we already talked about (Arrays, Lists, Trees, Hashtables etc.). It's pretty useful to use in problems that need finding the shortest path, calculating network flow and many others. A Graph is a way of representing the connectivity using nodes (or vertices) and edges that connect the nodes together. Our Nodes/Vertices will be labeled using numbers or letters of the alphabet. The Nodes and Edges can have some kind of information such as weight of travel and so on. So, a Graph contains a Set of Vertices and a Set of Edges!

Types:

    There are many types of Graphs and they are seperated depending on the Edges. For example if the Edges are bidirectional we have a Undirected Graph and if they are one-directional or directed we have a Directed Graph. We also have a Weighted Graph is the Edges contain a weight attribute. You actually don't have to know more then those 3 Types for our Algorithms later on!

Representation in memory:

    But, how do we store this connectivity between the Vertices? Well, there are 2 ways of representing this relationship between the Vertices. We can store this information inside of an Adjacency List or an Adjacency Matrix. In the first implementation each Vertex has a List of Vertices who are adjacent/direct neighbours with it. With a Matrix we represent the Edges-Adjacency using a boolean value of 0 when the Vertices are not connected and 1 or the weight value when they are connected. When having a sparse Graph the List implemenation is better, cause it's more space-efficient, but when having a dense Graph the Matrix implemenation is better! Most Algorithms use the List implementation, but in some Cases the Matrix implemenation is faster. So, we will implement both today in the most simplest way and extend upon it or tweak it depending on the algorithm we want to implement!

Basic Functionality:

    All Graphs need a specific Functionality. We need a function to add an Edge, remove an Edge and check for the existance of an Edge! We also need a way of getting the neighbours of a Vertex. Some like doing it using inEdge and outEdge functions, but I will keep it simple for today and just return the neighbours (for Lists we will just return the List of the corresponding Vertex and for the Matrix we will have to write a function that makes a List out of them). I will also include a basic print function. To keep our conding simple we will not use weight for the Edges and also have a Undirected Graph! That means that we will add 2 Edges (one for A->B and one for B->A for example).

Let's now get into the Implemenation part!

Matrix Implemenation:

    The Matrix implemenation is pretty simple. We will store the count of Vertices and have Double Matrix that will be of type boolean and store the existance information. Because we want to have a Undirected Graph I will add both opposing Edges and also remove them in deletion. Existance is simply checked by checking the corresponding square of the Matrix, cause it will return true or false. The neighbourhood can be found by searching the array column or row of the specific Vertex and inserting the Vertices of it's neighbourhood to a List that we return. Printing is also pretty self explanatory and will use the neighbourhood function and then print the neighbours of each Vertex!

So, our Code looks like this:

import java.util.List;

import java.util.ArrayList;

public class GraphMatrix {

    private int vCount;

    private boolean[][] adj;

    public GraphMatrix(int vCount) {

	this.vCount = vCount;

	adj = new boolean[vCount][vCount];

    }

    public void addEdge(int i, int j) {

	adj[i][j] = adj[j][i] = true;

    }

    public void removeEdge(int i, int j) {

	adj[i][j] = adj[j][i] = false;

    }

    public boolean hasEdge(int i, int j) {

	return adj[i][j];

    }

    public List<Integer> neighbours(int vertex) {

	List<Integer> edges = new ArrayList<Integer>();

	for (int i = 0; i < vCount; i++)

		if (adj[vertex][i])

			edges.add(i);

	return edges;

    }

    public void printGraph() {

	for (int i = 0; i < vCount; i++) {

		List<Integer> edges = neighbours(i);

		System.out.print(i + ": ");

		for (int j = 0; j < edges.size(); j++) {

			System.out.print(edges.get(j) + " ");

		}

		System.out.println();

	}

    }

}

List Implementation:

    The List implemenation is also not so difficult. We will again store the vertice count, but this time have a Array of Lists for the neighbours of each Vertex. To add a Edge we simply add the Vertex number/id to the corresponding List 2 times for each end of the Edge, cause we have a Undirected Graph. To delete we iterate through the List of both Vertices and remove the corresponding Vertex from both of them! To check for existance we use the List function contains. The neighbourhood is simply the List of the corresponding Vertex and printing is again the same as with the Matrix!

So, our Code looks like this:

import java.util.ArrayList;

import java.util.Iterator;

import java.util.List;

public class GraphList {

    private int vCount;

    private List<Integer>[] adj;

    public GraphList(int vCount) {

	this.vCount = vCount;

	adj = (List<Integer>[]) new List[vCount];

	for (int i = 0; i < vCount; i++)

		adj[i] = new ArrayList<Integer>();

    }

    public void addEdge(int i, int j) {

	adj[i].add(j);

	adj[j].add(i);

    }

    public void removeEdge(int i, int j) {

	Iterator<Integer> it = adj[i].iterator();

	while (it.hasNext()) {

		if (it.next() == j) {

			it.remove();

			break;

		}

	 }

	Iterator<Integer> it2 = adj[j].iterator();

	while (it2.hasNext()) {

		if (it2.next() == i) {

			it2.remove();

			return;

		}

	}

    }

    public boolean hasEdge(int i, int j) {

	return adj[i].contains(j);

    }

    public List<Integer> neighbours(int vertex) {

	return adj[vertex];

    }

    public void printGraph() {

	for (int i = 0; i < vCount; i++) {

		List<Integer> edges = neighbours(i);

		System.out.print(i + ": ");

		for (int j = 0; j < edges.size(); j++) {

			System.out.print(edges.get(j) + " ");

		}

		System.out.println();

	    }

    }

}

Testing both with same Example:

Let's test those Graphs now out on the same Example Graph and function callings!

public class TestGraphs {

    public static void main(String[] args) {

	GraphMatrix g1 = new GraphMatrix(5);

	System.out.println("Adjacency Matrix:");

	// add Edges

	g1.addEdge(0, 1);

	g1.addEdge(1, 3);

	g1.addEdge(1, 4);

	g1.addEdge(2, 3);

	g1.addEdge(3, 4);

	// check for existance of (1, 2)

	System.out.println("Graph has Edge (1,2) ? " + g1.hasEdge(1, 2));

	// remove Edge (1, 4)

	g1.removeEdge(1, 4);

	// print Graph

	g1.printGraph();

	GraphList g2 = new GraphList(5);

	System.out.println("\nAdjacency List:");

	// add Edges

	g2.addEdge(0, 1);

	g2.addEdge(1, 3);

	g2.addEdge(1, 4);

	g2.addEdge(2, 3);

	g2.addEdge(3, 4);

	// check for existance of (1, 2)

	System.out.println("Graph has Edge (1,2) ? " + g2.hasEdge(1, 2));

	// remove Edge (1, 4)

	g2.removeEdge(1, 4);

	// print Graph

	g2.printGraph();

    }

}

    Hope that you could see that there is absolutely no difference at all between those two implemenations when using the Graph in a Testing Programm like this! The differences will come visible when implementing algorithms! There you will see that the neighbourhood calculation will take a lot of time for the Matrix Implementation and that the Removal Process using Lists will also take a lot of time!

This is actually it! hope you enjoyed this post!

Until next time...Bye!