Programming - Java Graph Minimum Spanning Tree Algorithms 2
Hello it's a me again Drifter Programming! Today we get back to Java Graphs and Programming to talk about 2 more MST Algorithms! In my previous post about this topic we covered Prim's and Kruskal's MST algorithms. Today we will get into Boruvka's algorithm and the Reverse Delete (reverse Kruskal) Algorithm, where both will be implemented in Java!
So, without further do, let's get straight into it!
What is a Minimium Spanning Tree (MST)?
Before getting into the Algorithms we should first get back to what an MST is and how we use it and why we use it in real applications.
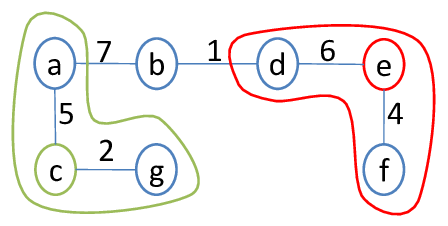
A graph is made up of vertices (or nodes) and edges, where the nodes are connected together using edges. The edges can be weighted and so we end up with weighted graphs and they can also be directional and so we can have directional graphs.
When using only some of the edges of a graph we can create a tree, called a Spanning Tree, that is subgraph of this graph that contains all the vertices, but doesn't contain cycles. The Spanning Tree with the least sum of weights is called a Minimum Spanning Tree (MST). The MST is not unique and we can have multiple ones that can all have the same sum of weights!
So, how can this be useful? Well, suppose we have a network where the computers/nodes have specific connections/edges with weights (connection delay, distance etc. can describe the connection). When a computer wants to send data to another computer it must send it using the best path so that is gets there in the least time possible and doesn't charge the network with too much load.
For example, using Prim's algorithm we can create a MST that starts from an specific node and find a tree that shows us the best way of sending packets from this node to the others, by following the edges of this tree. Off course, the Shortest Path algorithms like Dijkstra or Bellman-Ford, or even Floyd-Warshall and Johnson's algorithms that find the Shortest Path's for All Pair's are much more useful in such a application, but creating a tree can sometimes be faster and cheaper!
Previous Algorithms I covered
In my previous post about this topic I covered Prim's and Kruskal's MST Algorithms.
Let's recap them really quick, to see again how they work, so that the new ones that are similar to them can be understood more easily. I will not get into pseudocode, but just explain the idea behind them again, cause the implementation in code was already done in the previous post.
Prim's algorithm
In Prim's algorithm we start from an specific starting vertex/node that we set. We expand our Tree outwards by adding neighbour Edges of the current Tree that have the least weight and don't create cycles.
Kruskal's algorithm
In Kruskal's algorithm we don't start from an specific vertex/node, but insert the least-weighted edges to the Tree repeatedly (until a Tree is formed) and so that no cycles are created.
Both of these algorithms are greedy (or "dump") and find the solution using the optimal/best choice in each step. This means that the solution from a specific step is supposed optimal and can't be changed by a step that follows it!
Let's now get into today's algorithms!
Boruvka's Algorithm
Boruvka's algorithm is very similar to Prim's and is like a "parallel version" of Prim.
The steps we follow are:
- Start with a Forest (many Trees) where each Tree is a vertex/node of the given Graph
- Find the least-weighted neighbour edge that doesn't create a cycle for each Tree/vertex of the Forest and add it to it's Tree (so we don't start from one vertex like in Prim, but do it parallely in all the vertices at the same time)
- If the Trees (all the nodes) in the Forest are not connected together then find the least-weighted neighbour edge that doesn't create a cycle for each of those Trees (more vertices connected together) and add it to those Trees
- Continue step 3 until all the Trees in the Forest are connected together to create one Tree, the MST
Boruvka Java Implementation
To implement this we will use the same Graph implementation as in Prim.
The Edge class will contain one function more for getting the opposite Edge, that I don't implemented then, but simplifies some things!
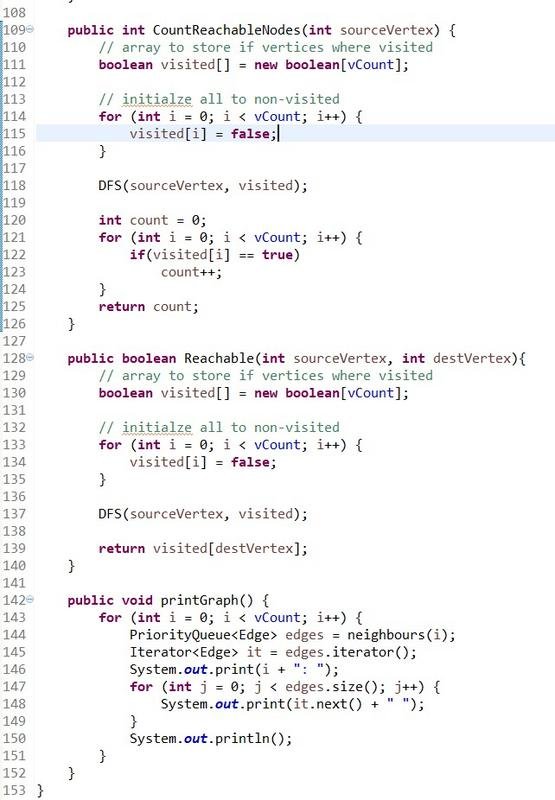
Our Graph will contain functions for:
- checking if everything is connected together aka isConnected()
- how many nodes are reachable starting from an specific node aka CountReachableNodes()
- if a node is reachable from an specific node aka Reachable()
where all will use DFS Traversal for that,
Because, it's easier without sets, I will use the following pseudocode/steps:
- Initialize MST to empty
- Loop until all nodes are connected by doing the next steps
- Loop through all vertices checking if all nodes are reachable from an specific node
- if not then iterate throuh all edges to add they least-weighted edge to the mst, that is not added already and will also don't create a cycle (endpoint is not reachable already)
So, our Classes are:
Edge:

Graph:


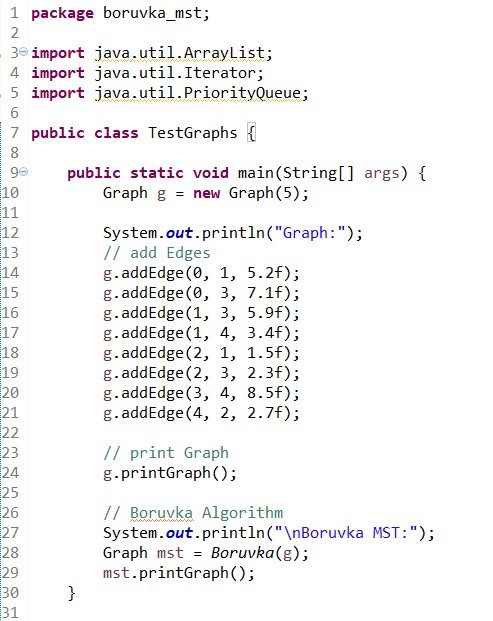
TestGraphs (Boruvka is here):

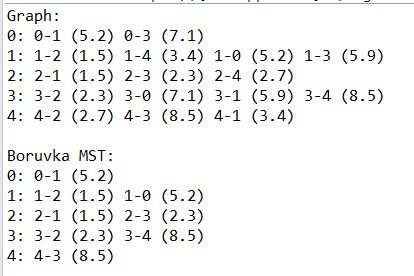
Console prints out:
Pastebin codes:
For this to work you have to put the code inside of a package with name: "boruvka_mst".
You can also just remove the first line from each class!
More about Boruvka's algorithm can be found at:
The first helped me remember some theory and the second one gave me an idea of how I can implement the algorithm in Java, by seeing how it's implemented in C and Python, and reading about the steps/pseudocode there!
Reverse Delete Algorithm
This Algorithm is like a reverse version of Kruskal.
In Kruskal we find and add the least-weighted edges in every step until we get the MST.
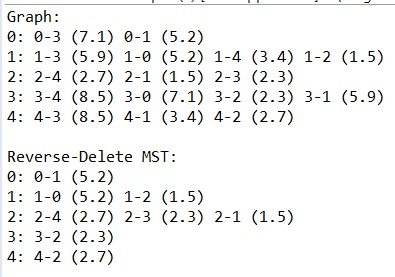
In the Reverse Delete Algorithm we remove the most-weighted edges of the Graph, so that the nodes stay connected together (graph must be cohesive/connected), but only the least-weighted edges remain and create a Tree, the MST.
Reverse Delete Java Implementation
We will use almost the same Graph implementation as in Kruskal (adjacency list).
The Edge will have an opposite() function again to get the opposite Edge quicker!
The Graph will use a isConnected() function that uses DFS (like in Boruvka) to check if removing an Edge (the current Edge) will cause the Graph to split!
Also, the edges will be inserted in decreasing order (and not increasing as done in Kruskal) by reverting the way the comparison function of the Edge class works.
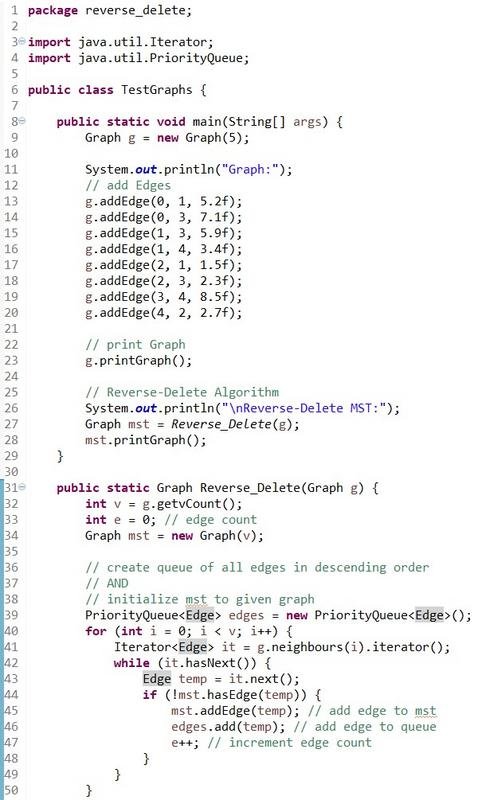
The pseudocode/steps that I will follow are:
- Initialize MST to given Graph AND create queue of all edges in descending order (by also using a counter to counter the number of edges inserted)
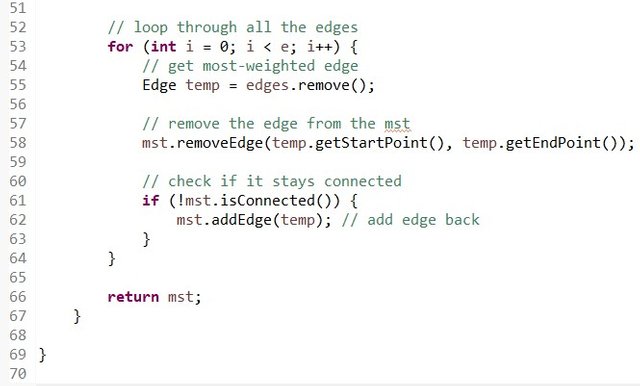
- Loop through all the edges continuously, by removing the most-weighted edge from the queue, finding and removing this edge also from the MST, checking if the MST stays connected and adding it back if it doesn't.
- After passing thorugh all edges the result will be our final MST
So, our Classes are:
Edge:

Graph:



TestGraphs (Reverse-Delete is here):
Console prints out:
Pastebin codes:
For this to work you again have to put the code inside of a package with name: "reverse_delete" or you can also just remove the first line from each class!
More about the Reverse-Delete algorithm can be found at:
The first one gave me the important and needed knowledge about the algorithm, and the second one gave me an C implementation and pseudocode/steps that helped me understand and implement the same algorithm in Java!
Image Sources:
The rest is Screenshots from Eclipse IDE!
And this is actually it and I hope that you enjoyed it!
I didn't upload about Programming in general for a long time now, but I will try to upload more often from now on! I have some ideas for more Graph Algorithms that I could implement in Java and explain, and I also want to continue with the Compiler series that can also be marked as Programming! This doesn't mean that I will stop with Mathematics or Physics, but it means that I will try to upload more Programming in between of that!
See ya!
