Programming - C Binary Trees
Today's subject are Binary Trees in C Implementation. We already did Linked Lists and you will see that the concept is similar and we will also do similar stuff to them. We will only talk about simple Trees and not about "self-fixing" Trees, like AVL, Red-Black, 2-3 Trees and so on...that use some concepts of the Binary Trees to make it more simple. I will show you how to insert, delete, search and print in 3 orders.
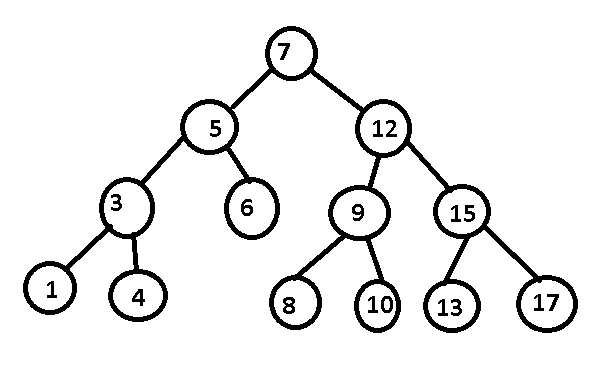
Binary Tree Represenation:
A Binary Tree is a Data Structure with Infinite Length were every TreeNode is pointing to at most 2 other TreeNodes called childs and we have 1 root of the Tree that is being saved in our function to access every other Node of our Tree. Something special about it is that the left child has always a value that is smaller then his parent's value and the right child has a value that is bigger than his parents value.
Every TreeNode has 2 Pointers to other TreeNodes called left and right and the Data. So, the Code will look like this:
typedef struct TNode{ //DATA struct TNode *left; struct TNode *right;}TNode;We will store the first TNode in our function the same way as we did with Lists initialized to NULL that means empty again, like this:
TNode *root = NULL;So, without further do let's start out with functions now.
Insert:
We will create a new TreeNode the same way as we did with Lists. The Code will look like this:
TNode *nn; nn = (TNode*)malloc(sizeof(TNode)); // for every Data Variable we do nn->val = val; // we set the pointers to NULL nn->left = NULL; nn->right = NULL;Because, we have some kind of sorting in our Tree were the left child is smaller and the right child is bigger we can use a insertion function that works similar to the binary search function (now you can see why I posted the stuff with recursive functions). Also, we only can have a value one time, but I will not put Code checking for this to make it simpler. The Code will look like this:
TNode* insert(TNode *root, int val){ TNode *nn; nn = (TNode*)malloc(sizeof(TNode)); // for every Data Variable we do nn->val = val; // we set the pointers to NULL nn->left = NULL; nn->right = NULL; // check if tree is empty if(root == NULL){ // return nn as our new root or // because of recursion it will set // the nn were it belongs in the tree return nn; } if(val < root->>val){ // call function again for left side root->left = insert(root->left, val); return root; } else if(val > root->va>){ // call function again for right side root->right = insert(root->right, val); return root; }}As you can see the Code is pretty simple when using recursion, else it would be really difficult to implement such behavior!
Delete:
To delete a Node the process is more complicated. We can have several Cases that could happen and we have to make sure that our Code can recognize all of them.
Node is Leaf
When our Node is at the bottom of our Tree and has no Childs then we simple have to set the parent's pointer to it to NULL.
Node has one child
When our Node has only child than we have to set the parent's pointer to it to it's child.
As you can see we can put both of them in one case, cause the child of the Leaf is NULL and so it makes the same operation.
Node has two childs
Then we have to find the Node that will replace it called successor, set the Node to be it's succesor and delete the "old"successor.
In Conclusion, we have to implement the following 2 Cases:
- Node has 0 or 1 Childs (we also check if it is left or right child)
- Node has 2 Childs (that includes finding the successor)
Let's first create some Code for finding the successor. The successor has a value that is exactly after the one we want to delete in the whole Tree. So, we first go the right child of the Node we want to delete (when calling this function) and afterwards find the child that is most left of it. The Code will look like this:
TNode* successor(TNode *node){ TNode *cur; // set cur to point to our node cur = node; // find the most left child while(cur->left != NULL){ // set cur to left pointer cur = cur->left; } // it returns the most left child return cur;}So, finally this is the Code for deleting a Node:
TNode* delete(TNode *node, int val){ // check if tree is empty if(node == NULL){ printf("Not found!\n"); return node; } if(val < node->val){ // call function again for left side node->left = delete(node->left, val); return node; } else if(val > node->>val){ // call function again for right side node->right = delete(node->right, val); return node; } else{ // when val was found (cases) // has left and right child if(node->left != NULL && node->right != NULL){ // find successor TNode *s = successor(node->right); // set value of Node to be deleted to successor's value node->val = s->>>>val; // delete successor node->right = delete(node->right, s->val); return node; } // has only left child else if(node->left != NULL){ // set node to it's child node = node->left; return node; } // has only right child else if(node->right != NULL){ // set node to it's child node = node->right; return node; } // has no child else{ // simply set node to be deleted to NULL node = NULL; return node; } } }We could also free some memory before setting to NULL and so on but nah! no need for such a simple Example.
Searching:
Searching is pretty simple and can be done using an recursive function similar to the insertion algorithm with the exception that we now return this node when find else we will return NULL that means not found. Code is the following:
TNode* search(TNode *root, int val){ // if empty or found at root if(root == NULL || root->val == val){ // return root return root; } // if smaller else if(val < root->val){ // call function again for left side return search(root->left, val); } // if greater else if(val > root->val){ // call function again for right side return search(root->right, val); }}Printing:
Last but not least I will show you how to print in preorder, inorder and postorder. All of those functions will use the same function, having only the printing switch place.
PreOrder:
Preorder is when you print the root's value and then the left and right child. So, the Code looks like this:
void preorder(TNode *root){ if(root == NULL) return; printf("%d ", root->val); if(root->left != NULL)inorder(root->left); if(root->right != NULL)inorder(root->right);}InOrder:
Inorder is when you print the left child then the root then the right child. The output will be in ascending order and the Code looks like this:
void inorder(TNode *root){ if(root == NULL) return; if(root->left != NULL)inorder(root->left); printf("%d ", root->val); if(root->right != NULL)inorder(root->right);}PostOrder:
Postorder is when you first print the left and right child and afterwards the root. Code looks like this:
void postorder(TNode *root){ if(root == NULL) return; if(root->left != NULL)inorder(root->left); if(root->right != NULL)inorder(root->right); printf("%d ", root->val);}Code:
Now for the end part, here a little programm that calls those functions so that you know how to call them.
int main(){ // initialize to NULL TNode *root = NULL; // insert some Nodes root = insert(root, 10); root = insert(root, 15); root = insert(root, 5); root = insert(root, 7); root = insert(root, 3); root = insert(root, 13); root = insert(root, 21); // delete some Nodes root = delete(root, 5); root = delete(root, 10); root = delete(root, 21); // search for 7 TNode *s; s = search(root, 7); if(s == NULL){ printf("Not found!\n"); } else{ printf("%d was Found!\n", s->val); } // print in all orders preorder(root); printf("\n"); inorder(root); printf("\n"); postorder(root); printf("\n");}This was the end of today's Tutorial. Hope you enjoyed it. Next time we will take a look into Stacks and Queues in Array Implementation and afterwards we do the same with Linked Lists. :)
Congratulations @drifter1! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPNice article
Would be interested in seeing a priority queue in C :)
Thank you! I will upload about Queues tomorrow.
Knowing the Basics you can make a priority Queue in no time.
I will put a hint or something if you want :)
I might do a mirror of these but show the structures in different languages. The binary tree structures are so easy in something like ML/F#/Haskell. So little code
I will reference your related articles if I create these to keep the context. See if we can get a load of interrelated ones for different languages by different people:)
Here you go. An immutable stack in C#