Linear Algebra In R
Hi there. This (long) post is about performing some linear algebra operations in the statistical programming language R.
Sections
- Part One: Vectors
- Part Two: Matrices
1) Vectors In R
Vector operations in R are not really difficult. I first define two vectors a and b.
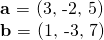
### Part One Vectors
a <- c(3, -2, 5)
b <- c(1, -3, 7)
Vector addition and vector subtraction does the addition/subtraction in an elementwise fashion.
> ## Vector addition (adds elementwise)
> a + b
[1] 4 -5 12
>
> ## Vector subtraction:
> a - b
[1] 2 1 -2
You can have vectors multiplied by a scalar/number.
> ## Vector multiplied by scalar (number):
> 2*a
[1] 6 -4 10
> 3*b
[1] 3 -9 21
> 2*a - 3*b #combo
[1] 3 5 -11
Dot Product
The dot product of two vectors consists of element wise multiplication and then taking the sum of the products.
> ## Dot Product of Two Vectors (Element wise multiplication and sum the products):
>
> a*b # Not good enough, gives the products of the elements
[1] 3 6 35
>
> sum(a*b) # Dot Product
[1] 44
>
> a*a # Element wise squares.
[1] 9 4 25
Cross Product
Given two vectors, the cross product vector is a third vector which is perpendicular/orthogonal to both the two vectors.
> ## Cross Product Of Two Vectors
> # https://stackoverflow.com/questions/36798301/r-compute-cross-product-of-vectors-physics
>
> p <- c(3, -1, 0)
> q <- c(-1, 0, 2)
>
> #install.packages("pracma")
> require("pracma")
Loading required package: pracma
>
> crossProd <- cross(p, q)
> crossProd
[1] -2 -6 -1
Checking Orthgonality
It can be verified that the cross product vector is truly a cross product vector by making sure that the two dot product s between the cross product vector and the other two vectors are zero.
> # Check orthogonality by checking that dot product is zero between cross product vector with p and q.
>
> sum(crossProd * p)
[1] 0
> sum(crossProd * q)
[1] 0
Vector Norms
There is no built in function in R for vector norms. The square root function with the sum function is used.
> ## Norm Of A Vector:
>
> c <- c(2, 0, -3, 5)
>
> sqrt(sum(c^2))
[1] 6.164414
Distance Between Two Vectors With Norms
Norms can also be used to compute distance between two vectors. There are three ways to do this in R.
> ## Distance Between Two Vectors With Norms
>
> # 2-D Case:
>
> v <- c(2, 0)
> w <- c(5, -3)
>
> sqrt(sum((v - w)^2)) # Option One
[1] 4.242641
>
>
> dist(rbind(v, w)) # Option Two
v
w 4.242641
>
>
> norm(v - w, type = "2") # Option Three
[1] 4.242641
> # 4-D Case:
>
> x <- c(1, -3, 4, -2)
> y <- c(2, -1, 0, 3)
>
> sqrt(sum((x - y)^2)) # Option One
[1] 6.78233
>
>
> dist(rbind(x, y)) # Option Two
x
y 6.78233
>
>
> norm(x - y, type = "2") # Option Three
[1] 6.78233
2) Matrices In R
To start, here are a few special matrices.
> # Matrix of Ones (n = 4):
>
> matrix(data = rep(1, times = 4^2), nrow = 4, ncol = 4)
[,1] [,2] [,3] [,4]
[1,] 1 1 1 1
[2,] 1 1 1 1
[3,] 1 1 1 1
[4,] 1 1 1 1
>
> # Matrix Of Zeroes(n = 5):
>
> matrix(data = rep(0, times = 5^2), nrow = 5, ncol = 5)
[,1] [,2] [,3] [,4] [,5]
[1,] 0 0 0 0 0
[2,] 0 0 0 0 0
[3,] 0 0 0 0 0
[4,] 0 0 0 0 0
[5,] 0 0 0 0 0
>
> # Identity Matrix (n = 5):
>
> diag(5)
[,1] [,2] [,3] [,4] [,5]
[1,] 1 0 0 0 0
[2,] 0 1 0 0 0
[3,] 0 0 1 0 0
[4,] 0 0 0 1 0
[5,] 0 0 0 0 1
The matrix() Command
In R, the matrix() command is a key command for creating matrices. You need to specify the matrix elements, the number of rows, the number of columns and whether or not you want the entries to go by row or not.
> A <- matrix(data = c(1, 2, 3, 4), nrow = 2, ncol = 2, byrow = FALSE)
> A
[,1] [,2]
[1,] 1 3
[2,] 2 4
>
> A <- matrix(data = c(1, 2, 3, 4), nrow = 2, ncol = 2, byrow = TRUE)
> A
[,1] [,2]
[1,] 1 2
[2,] 3 4
>
> B <- matrix(data = c(1, -5, 2, 0), nrow = 2, ncol = 2, byrow = TRUE)
> B
[,1] [,2]
[1,] 1 -5
[2,] 2 0
Matrix Multiplication
In R, you have to be careful in not being confused between element wise multiplication and matrix multiplication.
> A <- matrix(data = c(1, 2, 3, 4), nrow = 2, ncol = 2, byrow = TRUE)
> A
[,1] [,2]
[1,] 1 2
[2,] 3 4
>
> B <- matrix(data = c(1, -5, 2, 0), nrow = 2, ncol = 2, byrow = TRUE)
> B
[,1] [,2]
[1,] 1 -5
[2,] 2 0
>
> # Element Wise Multiplication
>
> A * B
[,1] [,2]
[1,] 1 -10
[2,] 6 0
>
> # Matrix Multiplication (Not the same as the above):
>
> A %*% B
[,1] [,2]
[1,] 5 -5
[2,] 11 -15
Transpose Of A Matrix
Given a matrix, the transpose of the matrix has the rows now being columns and columns being rows.
> # Transpose Of A Matrix (Switch rows with columns and vice versa):
>
> C <- matrix(data = c(1, -5, 2, 0, 2, 1, 1, -4, 2), nrow = 3, ncol = 3, byrow = TRUE)
> C
[,1] [,2] [,3]
[1,] 1 -5 2
[2,] 0 2 1
[3,] 1 -4 2
>
> t(C) #transpose
[,1] [,2] [,3]
[1,] 1 0 1
[2,] -5 2 -4
[3,] 2 1 2
Determinant Of A Matrix
The determinant of a matrix can be easily computed in R with the det() function.
> # Determinant of the C Matrix:
>
> det(C)
[1] -1
(The determinant is non-zero. This means that the matrix C is invertible and a matrix inverse exists.)
Lower And Upper Triangular Matrices
A lower triangular matrix has the entries above the main diagonal being zero. The main diagonal and the entries below the diagonal can be anything.
> # Lower Triangular Matrix:
>
> Y <- matrix(data = c(2, 0, 1, 1, -4, 5, 2, 3, 8), nrow = 3, ncol = 3, byrow = TRUE)
> Y
[,1] [,2] [,3]
[1,] 2 0 1
[2,] 1 -4 5
[3,] 2 3 8
>
> Y[upper.tri(Y)] <- 0
>
> Y
[,1] [,2] [,3]
[1,] 2 0 0
[2,] 1 -4 0
[3,] 2 3 8
Inverse Of A Matrix
The solve() command is for finding the inverse of a matrix.
> # Inverse Of The C Matrix
>
> solve(C)
[,1] [,2] [,3]
[1,] -8 -2 9
[2,] -1 0 1
[3,] 2 1 -2
>
> solve(C) %*% C # Check by matrix multiplication to get identity matrix
[,1] [,2] [,3]
[1,] 1 0 0
[2,] 0 1 0
[3,] 0 0 1
Diagonal Entries Of A Matrix & The Trace Of The Matrix
The main diagonal of a matrix consists of the middle entries going from the top left to the bottom right. Computing the sum of these main diagonal entries gives the trace of a matrix.
The diag() command outputs the main diagonal entries. Combining diag() with sum() gives the trace of a matrix.
> # Diagonal entries of the C matrix:
>
> diag(C)
[1] 1 2 2
>
> sum(diag(C)) #Trace of C matrix
[1] 5
Lower & Upper Triangular Matrices
A lower triangular matrix has entries above the main diagonal being zero. Entries along the main diagonal and below it can be any number (including zero).
> # Lower Triangular Matrix:
>
> Y <- matrix(data = c(2, 0, 1, 1, -4, 5, 2, 3, 8), nrow = 3, ncol = 3, byrow = TRUE)
> Y
[,1] [,2] [,3]
[1,] 2 0 1
[2,] 1 -4 5
[3,] 2 3 8
>
> Y[upper.tri(Y)] <- 0
>
> Y
[,1] [,2] [,3]
[1,] 2 0 0
[2,] 1 -4 0
[3,] 2 3 8
An upper triangular matrix has entries below the main diagonal being zero. Entries along the main diagonal and below it can be any number (including zero).
> # Upper Triangular Matrix:
>
> Z <- matrix(data = c(1, 3, -2, 5, 6, 7, 1, 0, 3), nrow = 3, ncol = 3, byrow = TRUE)
>
> Z[lower.tri(Z)] <- 0
>
> Z
[,1] [,2] [,3]
[1,] 1 3 -2
[2,] 0 6 7
[3,] 0 0 3
Eigenvalues & Eigenvectors Of A Matrix
The eigen() function gives the eigenvalues and eigenvectors of a matrix. Refer to the $val component for eigenvalues and refer to the $vec for the eigenvectors.
You may get some complex numbers in the output. The format is in a + bi format.
> # Eigenvalues & eigenvectors of the C matrix:
>
> C <- matrix(data = c(1, -5, 2, 0, 2, 1, 1, -4, 2), nrow = 3, ncol = 3, byrow = TRUE)
> C
[,1] [,2] [,3]
[1,] 1 -5 2
[2,] 0 2 1
[3,] 1 -4 2
>
> y <- eigen(C)
>
> y$val # eigenvalues
[1] 2.54768297+1.998809i 2.54768297-1.998809i -0.09536594+0.000000i
> y$vec # eigenvectors
[,1] [,2] [,3]
[1,] 0.6927678+0.0000000i 0.6927678+0.0000000i -0.9637826+0i
[2,] 0.0432013-0.3104024i 0.0432013+0.3104024i -0.1148651+0i
[3,] 0.6440957-0.0836510i 0.6440957+0.0836510i 0.2406845+0i
References
http://dkmathstats.com/5703-2/ (One of my old/original articles)
Elementary Linear Algebra 10th Edition By Howard Anton
R Documentation
https://stackoverflow.com/questions/36798301/r-compute-cross-product-of-vectors-physics
Linear Algebra took me 2 classes to learn. Haha. The first time I took it, it was so bad for the class, the teacher didn't even give back the last two tests. When I took it in my masters program it came to me. Maybe I'll post some proofs from notes. Haha.
Sometimes the teacher makes the difference on your grade and perception of the subject.
I have mixed views on linear algebra. My first course on linear algebra was an intro course so it was easy for me. Linear Algebra Two was bad for me as it was more theoretical. I was somewhat bad in that.
When it comes to computational linear algebra, I'm okay at it. I like the computing side of linear algebra better than the abstract side of it.
I feel like the computation LA is easy. Haha. Introduced to it in 9th grade algebra two. Carried me through the first test, got 100. Again the 2nd and 3rd were bad, all theoretical!
Wow, thorough and interesting post. I will check out this programming language.
Thank you. You can also do linear algebra in Python with Numpy.