The Normal Distribution - Compute and visualize in Java

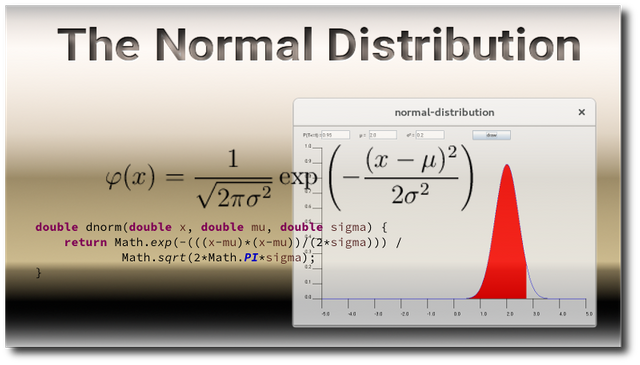
Hi, I'm in the process of extending my student's t-distribution program to other distributions. As the first extension I implemented the normal distribution. The normal distribution class is largely identical to the student t-distribution class. That is why I only show the most important differences here.

New variables

    double mu = 0;
    double sigma = 1;

Changes in the GUI

            labelMu = new JLabel();
            labelMu.setText("µ = ");
            labelMu.setBounds(175, 10, 50, 25);
            jPanel.add(labelMu);

            textFieldMu = new JTextField();
            textFieldMu.setText("0.0");
            textFieldMu.setBounds(200, 10, 75, 25);
            jPanel.add(textFieldMu);
            
            labelSigma = new JLabel();
            labelSigma.setText("σ² = ");
            labelSigma.setBounds(300, 10, 50, 25);
            jPanel.add(labelSigma);

            textFieldSigma = new JTextField();
            textFieldSigma.setText("0.0");
            textFieldSigma.setBounds(325, 10, 75, 25);
            jPanel.add(textFieldSigma);
            
            buttonDraw = new JButton();
            buttonDraw.setText("draw");
            buttonDraw.setBounds(475, 10, 100, 25);
            buttonDraw.addActionListener(new ActionListener() {
                public void actionPerformed(ActionEvent evt) {
                    mu = 0.0;
                    sigma = 1.0;
                    alpha = 0.95;
                    try {
                        mu = Double.parseDouble(textFieldMu.getText());
                        sigma = Double.parseDouble(textFieldSigma.getText());
                        alpha = Double.parseDouble(textFieldAlpha.getText());
                    } catch (Exception e) {
                        
                    }
                    daten = new double[w];
                    for (int i=0; i<w; i++) {
                        daten[i] = dnorm(-5.0+(10.0/w)*i, mu, sigma);
                    }
                    repaint();
                }
            });

Calculation of the distribution

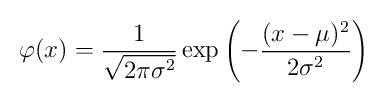
    double dnorm(double x, double mu, double sigma) {
        return Math.exp(-(((x-mu)*(x-mu))/(2*sigma))) /
                Math.sqrt(2*Math.PI*sigma);
    }
    
    public double qnorm(double alpha, double mu, double sigma) {
        double sum = 0;
        double pos = -1000;
        double stepSize = 0.01;
        while (sum<alpha) {
            sum += dnorm(pos, mu, sigma)*stepSize;
            pos += stepSize;
        }
        return pos;
    }