Great image compression method - JPEG
Using of new classes of images is the main trend in recent years. Older algorithms no longer meet the requirements of archiving. Many of the images were not compressed, although they had obvious redundancy. This led to the creation of a new type of algorithms - compressing with a loss of information. Generally, archiving ratio and hence the degree of loss of quality can be specified therein. This achieves a compromise between size and quality of images.
Lossy compression is based on the peculiarities of human vision. We will talk about the basic ideas of the JPEG image compression algorithm.
The algorithm is designed to compress the 24-bit image. In general, the algorithm is based on the discrete cosine transform (DCT) that is applied to the image matrix to get a new coefficient matrix. The inverse transformation is used for the original image.
DCT decomposes the image with the amplitudes of certain frequencies. Thus, after transformation, we obtain the matrix in which many ratios are either close or equal to zero. Moreover, thanks to the imperfections of human vision, the coefficients can be approximated more coarsely without noticeable loss of image quality.
For this purpose, the quantization of coefficients is used. In the simplest case – it is a bitwise arithmetic shift to the right. With this transformation, some information is lost, but great compression ratios can be achieved.
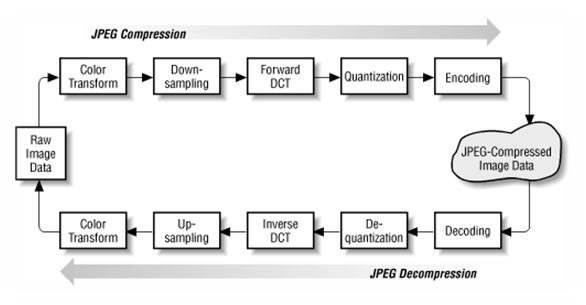
The work of algorithm
Firstly
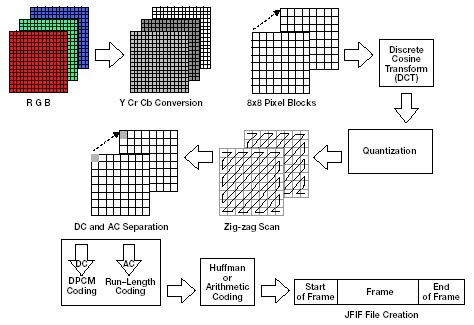
We transfer the image from RGB color space, with the components responsible for the red (Red), green (Green) and blue (Blue) components of the point color to the YCrCb(YUV) color space.
There Y – is a luminance component, and Cr, Cb - components responsible for color (chroma red and chroma blue). Due to the fact that the human eye is less sensitive to color than it is to brightness, it becomes possible to archive arrays for Cb and Cr components with high losses and correspondingly large compression ratios. This transformation has long been used in television.
Simplistically transferring from RGB color space into a YCrCb color space can be represented by a transition matrix:
Further
We divide the original image into a matrix of 8x8. Form three 8 bits DCT matrix separately for each component. The image is divided by the component Y - as in the first case, and for Cr and Cb components matrix are written in line or in the column. Those one working DCT matrix can be obtained from the original matrix with the size of 16x16. At the same time, we lose 3/4 of useful information about the color components of the image and get a twice compression.
Then
We use DCT to each operating matrix. We get a matrix in which the coefficients in the upper left corner correspond to the low-frequency component of the image, and in the bottom right - high frequency.
After
We make quantization. Basically, it's just the division of used matrix by quantization matrix element-wise. For each component (Y, U, and V), its own quantization matrix q [u, v] (QM) is set.
In this step occurs the compression ratio control, and the greatest losses occur. It is understood that by setting the QM with large coefficients, we obtain more zeros and hence a greater degree of compression.
The JPEG standard includes recommended QM built empirically. Matrices for larger or smaller compression ratios are obtained by multiplying the original matrix by a number of “gamma”.
Specific effects of the algorithm are associated with quantization. For large values of the coefficient of gamma loss in the low frequencies can be so high, that the image will break up into squares 8x8. The loss in high frequencies may occur in the so-called "Gibbs effect" when there are loops with a sharp transition of color that forms a kind of "halo".
Now
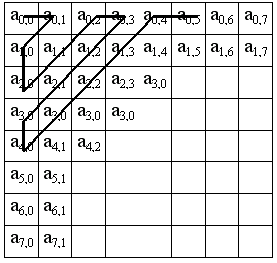
Transfer 8x8 matrix into a 64-element vector taking the elements with indices (0,0), (0,1), (1,0), (2,0) ...
Thus, in the beginning of the vector, we obtain the coefficients of the matrix corresponding to the low frequencies, and in the end - high.
Further
We roll vector with an algorithm using group coding. At the same time, we get pairs of type (skip, number), where "skip" is a counter of skipped zeros, and "number" - a value that must be put into the next cell. Thus, vector 42 3 0 0 0 -2 0 0 0 0 1 ... will be rolled into a pair (0,42) (0,3) (3, -2), (4,1) ....
Lastly
We roll the resulting pairs withHuffman encoding with a fixed table.
The process of restoring the image in this algorithm is completely symmetrical. The method is capable of compressing images 10-15 times without serious loss.
Positive sides:
- The compression ratio can be set.
- The output color of the image may have 24 bits per pixel.
Negative sides:
- With the increase of the degree of compression the image breaks up into individual squares (8x8).
In conclusion, I would like to show you the trend of development of algorithms in recent years:
- Focusing on photorealistic images with 16 million colors (24 bits);
- The use of lossy compression;
- The use of redundancy in the two-dimensional images;
- The appearance of asymmetrical algorithms;
- Increasing the degree of image compression.
References: 1
Follow me, to learn more about popular science, math and technologies
With Love,
Kate

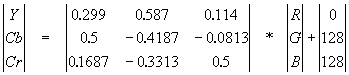

You are brilliant friend @ krishtopa, is not only a brilliant post ud do things Cillas sen to understanding all very practical in its redacciony that makes her formidable work my congratulations and thanks for sharing this majestic post
Thanks again for reading my posts. I'm flattered that have so many followers who are interested in popular science topic