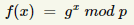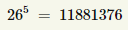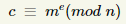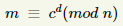Wprowadzenie do kryptografii
Uwaga: Jest to tekst który przygotowałem jakiś czas temu. Przed pisaniem tego artykułu miałem praktycznie zerową wiedzę na ten temat, więc bardzo możliwe, że jest tu wiele błędów rzeczowych. Nie traktujcie tego jako źródła naukowego ;D
"Żyjemy w społeczeństwie fundamentalnie uzależnionym od nauki i technologii, w którym mało kto ma jakiekolwiek pojęcie o nauce i technologii."
~ Carl Sagan, astronom i popularyzator nauki.
Coś o arytmetyce modularnej;
Nim wkroczymy w magiczny świat kryptografii musimy poznać coś, co matematycy nazywają arytmetyką modularną bądź arytmetyką reszt. Łatwo domyślić się, że chodzi tu o resztę z dzielenia... Tak, do tego to się sprowadza.
Przy dzieleniu dwóch liczb całkowitych występuje reszta:
A/B = Q reszty R
Jeśli interesuje nas tylko reszta z dzielenia możemy zastosować operator modulo, wtedy możemy zapisać:
A mod B = R
Co oznacza, że działanie A/B ma resztę równą R. B jest określane jako moduł. Załóżmy, że mamy:
21/37 = 0 reszty 21
Można to zapisać w następujący sposób:
21 mod 37 = 21
Zanim przejdziemy do zastosowania arytmetyki modularnej w kryptografii zobaczmy jak można zobrazować arytmetykę reszt za pomocą okręgów, np. 12 godzinnego zegara: załóżmy, że idziesz spać o godzinie 23, czyli wskazówka godzinowa zegara wskazuje 11. Śpisz 9 godzin, a wskazówka zegara pokazuje 8 mimo, że 9 + 8 = 17. Możemy to opisać za pomocą arytmetyki modularnej. Moduł w zegarze jest równy 12.
11+9 ≡ 8(mod 12)
Równość ta nazywana jest kongruencją, a czytamy ją "20 przystaje do 8 modulo 12". Możemy wyróżnić własności kongruencji takie jak:
- zwrotność kongruencji:
a ≡ a(mod n) - symetryczność kongruencji:
a ≡ b(mod n) ⇒ b ≡ a(mod n) - przechodność kongruencji:
(a ≡ b(mod n) ∧ b ≡ c(mod n)) ⇒ a ≡ c(mod n)
Słowo o funkcjach jednokierunkowych;
Funkcją jednokierunkową nazywamy funkcję, którą łatwo obliczyć, ale trudno jest obliczyć jej wartość funkcji odwrotnej. Oznacza to, że znając wartość x łatwo obliczyć jest f(x), ale znając f(x) trudno jest obliczyć oryginalną wartość x. Pierwiastkiem pierwotnym modulo n nazywamy taką liczbę, której potęgi dają wszystkie możliwe reszty modulo n. Arytmetyka modularna okazuje się być świetnym źródłem funkcji jednokierunkowych, np: Jeśli p jest liczbą pierwszą, a g jest pierwiastkiem pierwotnym modulo p, przy czym g < p i x < p, to:
jest funkcją jednokierunkową.
Funkcja Eulera to funkcja przypisująca dowolnej liczbie naturalnej liczbę liczb względnie z nią pierwszych mniejszych lub równych n, np.
φ(8) = 4
ponieważ 1, 3, 5 i 7 nie mają z 8 wspólnego dzielnika. Funkcja Eulera jest multiplikatywna, czyli dla dowolnych dwóch liczb względnie pierwszych a oraz b zachodzi zależność:
φ(a×b) = φ(a)×φ(b)
Dodatkowo, jeśli p jest liczbą pierwszą, to:
φ(p) = p−1
Kryptografia;
We współczesnym świecie, w którym dużą rolę odgrywa przekazywanie informacji drogą elektroniczną niezwykle trudne jest zachowanie prywatności. Większość naszych wiadomości może być przechwycona przez osoby trzecie. I tu wkracza kryptografia, czyli wiedza o utajaniu wiadomości.
Istotą szyfrowania tekstu jawnego, bo tak nazywamy naszą wiadomość w postaci zrozumiałej dla człowieka, jest to, aby osoba trzecia do której wiadomość nie jest kierowana, lecz która przechwyciła szyfrogram, czyli wiadomość już zaszyfrowaną nie była w stanie jej zrozumieć ani odszyfrować. Zanim przejdziemy do współczesnych metod kryptograficznych warto poznać metody historyczne, które są proste i dzięki nim łatwo zrozumieć idee szyfrowania wiadomości.
Szyfr Cezara;
Zwany także szyfrem przesuwającym, ponieważ jego działanie polega na tym, że każdą literę tekstu jawnego zastępujemy inną, oddaloną od niej o stałą liczbę pozycji w alfabecie z zachowaniem kierunku przesunięcia. Dlatego np. z litery B przy przesunięciu 13 otrzymamy O. Należy pamiętać, że najczęściej rozpatrujemy alfabet o 26 znakach, bez znaków polskich. Szyfowanie możemy wtedy zapisać za pomocą wzoru:
E(x) = (x+k) mod 26
gdzie x jest numerem litery tekstu jawnego w alfabecie, E(x) numerem litery po zaszyfrowaniu a k kluczem, czyli stałą przesunięcia. Aby odszyfrować wiadomość korzystamy ze wzoru:
D(y) = (y−k) mod 26
Gdzie y jest numerem litery szyfrogramu w alfabecie, D(y) numerem litery po deszyfrowaniu, czyli numerem litery tekstu jawnego, a k jest kluczem zastosowanym przy szyfrowaniu wiadomości. Jest to szyfr monoalfabetyczny co oznacza, że dla całej wiadomości używamy tego samego n, czyli liczby przesunięcia. Nazwa szyfru pochodzi od Gajusza Juliusza Cezara, który z kluczem k = 3 szyfrował korespondencje do swoich przyjaciół. Jest to szyfr, który bardzo łatwo złamać, czym zajmuje się kryptoanaliza. Można go złamać za pomocą algorytmu siłowego, czyli za pomocą sprawdzenia wszystkich możliwości przesunięć i sprawdzeniu przy którym przesunięciu wiadomość ma sens.
Szyfr z kluczem jednorazowym;
Jego działanie polega na tym, że generujemy ciąg liczb losowych o długości równej bądz większej niż długości tekstu jawnego, następnie każdą literę szyfrujemy analogicznie do szyfru Cezara za pomocą wzoru:
E(x) = (x+k) mod 26
gdzie x jest numerem litery tekstu jawnego w alfabecie, k jest wygenerowaną liczbą losową o tym samym numerze w kolejności ciągu co numer kolejności litery w tekście jawnym. E(x) jest zaszyfrowanym numerem litery w alfabecie. Załóżmy, że wiadomość ma tylko 5 znaków. Generujemy więc ciąg składający się z 5 liczb liter, załóżmy że jest to "EMVOA", następnie zamieniamy litery na odpowiadające im liczby w alfabecie - {5, 13, 22, 15, 1}. Naszą wiadomością niech będzie "STEEM". Zamieńmy teraz tekst na odpowiadający mu ciąg liczb, S jest 19 literą alfabetu, więc odpowiada jej właśnie liczba 19. Otrzymujemy ciąg: {19, 20, 5, 5, 13}. Następnie przechodzimy do szyfrowania naszej wiadomości za pomocą wygenerowanego klucza jednorazowego:
E1(x)=(x+k) mod 26 = (19+5) mod 26 = 24
E2(x)=(x+k) mod 26 = (20+13) mod 26 = 7
E3(x)=(x+k) mod 26 = (5+22) mod 26 = 1
E4(x)=(x+k) mod 26 = (5+15) mod 26 = 20
E5(x)=(x+k) mod 26 = (13+1) mod 26 = 14
Otrzymaliśmy ciąg: {24, 7, 1, 20, 14}, po podstawieniu odpowiadających liter alfabetu otrzymujemy szyfrogram: "XGATN".
Możecie się zastanawiać ile może być możliwości odszyfrowania tej krótkiej wiadomości dla osoby, która nie zna jednorazowego klucza. Z pomocą przychodzi nam kombinatoryka. Dla wiadomości pięcioznakowej będzie to:
możliwości. Im wiadomość a zarazem klucz jest dłuższy, tym trudniej jest zastosować algorytm siłowy.Przy poprawnym wykorzystaniu jest to szyfr technicznie niemożliwy do złamania bez znajomości klucza. Stosuje się go do szyfrowania wyjątkowo tajnych informacji, jest np. Stosowany w gorącej linii miedzy prezydentami USA i Rosji. Szyfr z kluczem jednorazowym ma też wady. Największą z nich jest to, że odbiorca musi się wcześniej fizycznie z nadawcą, aby ustalić klucz szyfrujący, który jest jednocześnie kluczem deszyfrującym.
Wraz z rozwojem sieci komputerowych pojawił się problem. Do tej pory aby nadawca i odbiorca, będziemy nazywać ich od teraz Alicja i Bob, mogli szyfrować swoje korespondencje musieli przynajmniej raz się spotkać i ustalić zbiór kluczy jednorazowych. I tu pojawia się problem - co jeśli Alicja i Bob nigdy się nie spotkają? Musimy więc znaleźć sposób na to, aby Alicja i Bob mogli ustalić klucz tak, aby Ewa, która podsłuchuje wszystkie ich korespondencje nie miała dostępu do ustalonego za pomocą matematyki klucza.Aby ustalić ten klucz możemy użyć np. protokołu Diffiego-Hellmana. Algorytm protokołu wygląda następująco:
- Alicja i Bob wspólnie ustalają liczbę pierwszą p oraz bazę g.
- Alicja wybiera losową liczbę całkowitą a (klucz prywatny Alicji).
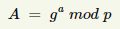
- Bob wybiera losową liczbę całkowitą b (klucz prywatny Boba).
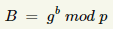
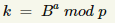
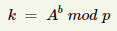
- Alicja i Bob współdzielą sekretną liczbę k, której Ewa bez znajomości conajmniej jednego klucza prywatnego nie jest w stanie odtworzyć!
Przy dużych liczbach w kluczach prywatnych oraz dużej liczby pierwszej p, znalezienie liczby k bez znajomości przynajmniej jednego klucza prywatnego jest technicznie niemożliwe co oznacza, że potrzeba wielkiej mocy obliczeniowej i bardzo dużo czasu aby znaleźć tę liczbę.
RSA;
RSA to asynchroniczny algorytm kryptograficzny z kluczem publicznym. Jego nazwa pochodzi od nazwisk twórców, którzy w 1977 roku zaprojektowali RSA: Rona Rivesta, Adi Szamira oraz Leonarda Adlemana. Algorytm generowania pary kluczy(publicznego i prywatnego) wygląda następująco:
- Wybieramy dwie duże liczby pierwsze p i q.
- Obliczamy:
n = p×q - Obliczamy:
φ(n)=(p−1)(q−1) - Wybieramy liczbę e, która jest względnie pierwsza z φ(n), taką, że:
1 < e < φ(n) - Znajdujemy taką liczbę d, że
d×e ≡ 1(mod φ(n)) - Wygenerowaliśmy klucz prywatny (n, d) oraz klucz publiczny (n, e)!
Teraz aby zaszyfrować wiadomość m o wartości liczbowej nie większej niż n wystarczy zaszyfrować ją według wzoru:
Aby szyfrogram przekształcić na tekst jawny należy użyć następującego wzoru:
Teraz każdy może wysłać nam zaszyfrowaną wiadomość, ponieważ klucz publiczny możemy udostępnić bez obaw o bezpieczeństwo.
Ten szyfrogram będziemy mogli odczytać tylko my za pomocą klucza prywatnego.
Słowo na koniec;
jeśli udało Ci się przeczytać cały artykuł to gratuluje ;] Jeśli zauważyłeś jakieś błędy - napisz komentarz, z chęcią je poprawię.