Spektroskopia dla (nie) kompletnie zielonych #8 Energie: Energia oscylacyjna

Są różne typy strasznych nocy, noc w opuszczonym dworku gdzie za każdym rogiem coś skrzypi, noc w zimnym lesie z dala od cywilizacji i najstraszniejsza ze wszystkich nocy - noc przed egzaminem który musimy zdać jeśli jeszcze chcemy pozostać na uczelni. Jeśli trafiłeś tutaj przypadkiem, radzę zamknąć tę kartę i zająć się czymkolwiek innym, obejrzeć film, wyjść na spacer, nauczyć się grać na pianinie. Nie znajdziesz tutaj niczego co mogłoby być w chociaż najmniejszym stopniu interesujące. Jeśli jednak chcesz zagłębić się w tą nieprzyjemną opowieść, zalecam lekturę poprzednich części ponieważ ta jest najgorsza, a będzie jeszcze gorzej.

Wydawać Wam się mogło, że widmo rotacyjne nie było takie straszne, owszem nie było, ponieważ wydawca zabronił mi wspominać o większości szczegółów. Dostaliście więc wersję ocenzurowaną. W tej części jednak nie miał takich zastrzeżeń, a może nie wyszedł wciąż z szoku? W każdym razie mogę napisać co tylko chcę.

Tym razem zajmiemy się Energią oscylacji. Zachodzi ona nie tylko w gazie, ale też w cieczy (i ciele stałym, ale to mniej istotne) Pozwala to nam w wygodny sposób badać substancje za pomocą spektroskopii IR i Ramana. (O nich opowiemy sobie dopiero za jakiś czas)

O co w ogóle chodzi z oscylacjami?

Wyobraźmy sobie sprężynę jak na zdjęciu. Bierzemy dwie osoby i każemy im złapać za końce ale nie ciągnąć. To będzie nasze położenie zerowe, gdzie energia sprężyny jest najmniejsza. Następnie każemy im pociągnąć za tę sprężynę do siebie. Sprężyna rozciąga się aż osiągnie jakieś maksimum. Wtedy energia potencjalna jest duża bo sprężyna jest naciągnięta i w każdej chwili może wrócić do położenia równowagi, a nawet dalej. Każemy następnie osobom aby spróbowały ścisnąć sprężynę. Łatwo wraca do stanu równowagi, ale im mocniej się ją ściska tym jest trudniej, i podobnie mamy tutaj znów dużą energię potencjalną, bo sprężyna może wrócić do położenia równowagi bardzo łatwo, a nawet polecieć trochę dalej.

W ten sposób działają oscylacje w cząsteczkach, są w położeniu równowagi, oddalają się na pewną odległość i znów wracają.

Ale, ale ktoś powie, że przecież może sobie, hehe, wygiąć tak sprężynę, że będzie z niej drut. I rzeczywiście tak jest, przy wyższych poziomach oscylacji, gdy odległości między cząsteczkami są duże, może zajść zjawisko zerwania wiązania, lub znacznego go wydłużenia, co z kolei powoduje powstanie oscylatora aharmonicznego, którego dokładny opis jest bardzo trudny.

Źródło
Oscylator harmoniczny dobrze reprezentuje ta animacja, kulka wychyla się z położenia równowagi i do niego wraca, drgając w kierunku ściskania i rozciągania na pewnym poziomie. Im większe są wychylenia i ściski, tym większa jest energia i wyższy poziom, który jak przeczuwamy, jest skwantowany. Przejście zawsze następuje pomiędzy sąsiednimi poziomami, tzn. +/- 1. Warto zauważyć, że wychylenia kulki w stronę ścisku rosną powoli i są mniejsze niż w kierunku rozciągania. Prowadzi to w konsekwencji właśnie do powstania oscylatora aharmonicznego w przypadku wyższych poziomów, a w przypadku nawet niskich, oscylator harmoniczny jest jedynie przybliżeniem, gdzie obowiązuje prawo Hooke'a

Przyczyną tych drgań są zmiany energii potencjalnej na kinetyczną i na odwrót. Przyczyną tego jest odpychanie się od siebie elektronów oraz przyciąganie przez oddziaływania kulombowskie.

Wprawne oko, zauważy też, że liczby falowe są bardzo duże, oznacza to krótkie fale, co z kolei oznacza bardzo dużą częstotliwość drgań, liczoną w setkach bilionów drgań na sekundę. To wszystko się rusza zawsze, nie staje nawet w zerze absolutnym, gdzie układ osiąga wartość kwantu połówkowego czyli 1/2 hv

Teraz skoro wiemy, że drga, musimy zadać sobie pytanie: Jak? Otóż sprawa nie jest taka prosta. Drgania opisane są przez stopnie swobody. Cząsteczka ma ich 3N, gdzie N to liczba atomów. 3 z nich przypadają na ruch translacyjny, a kolejne 3 (lub 2 w liniowych) na rotacyjny. Pozostałe są wolne dla oscylacji. Wynika stąd więc, że oscylator będzie miał 3N - 6(5) stopni swobody. Przykładowo dla cząsteczki 3 atomowej, możliwe będą 3 stopnie swobody. Cząsteczka może więc poruszać się w 3 kierunkach, może rozciągać swoje wiązanie, czyli poruszać się w kierunku osi y, może "machać" czyli poruszać się w osi x, a także wychodzić za i pod płaszczyznę, czyli poruszać się w osi z.

Obrazują to poniższe gify:


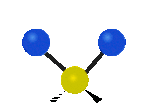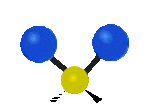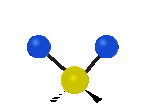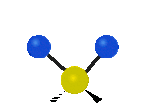
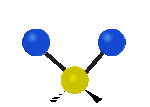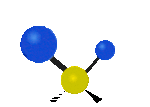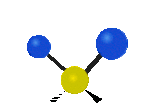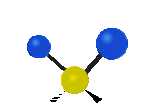
Te dwa należą do drgań poza płaszczyznę (w osi z), pierwsze jest drganiem wachlarzowym, natomiast drugie jest drganiem skręcającym.

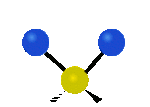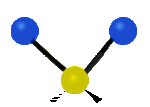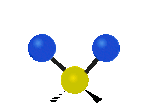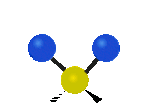
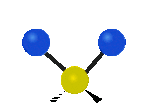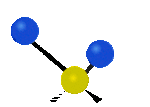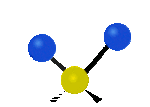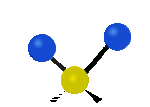
Tutaj mamy do czynienia kolejno z drganiem rozciągającym symetrycznym oraz rozciągającym asymetrycznym, oba w osi y.

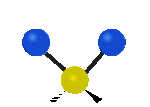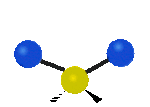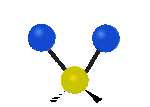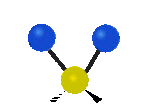
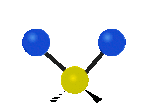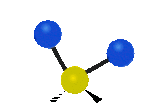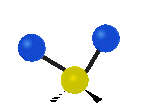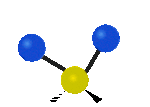
Na koniec drgania w osi x, pierwsze jest to drganie nożycowe w którym atomy nawzajem przybliżają się i oddalają, a drugie jest to drganie wahadłowe.
Źródło

Dobrze, skoro już wiemy jak wyglądają drgania i o co chodzi z oscylatorem harmonicznym, rozwiniemy to sobie. Otóż wróćmy na chwilę do animacji na początku:

Spójrzcie na linie poziomów, im wyższy poziom tym mniejsze różnice odległości pomiędzy poziomami. Można sobie to wyobrazić jako coraz większe rozciąganie sprężyny, gdzie coraz mniejsze zmiany siły powodują coraz większe odkształcenie, aż do zerwania, gdzie energia potencjalna zmienia się na energię translacji. Istotą tej informacji jest to, że w oscylatorze aharmonicznym przerwy energetyczne nie są jednakowe i maleją wraz z rosnącą energią.

Teraz zajmiemy się regułami wyboru. Dla oscylatora harmonicznego było to +/- 1, przy aharmonicznym nie jest tak łatwo ponieważ reguła ta może zostać nagięta i przejście może odbyć się, dalej, na +/- 2,3,4,5 itp. Przejścia absorpcyjne, czyli te z "+" nazywamy tonami - podobnie jak w akustyce. Przejście o +1 to ton podstawowy. Jest on najbardziej prawdopodobny ponieważ wymaga najmniejszej energii. Mogą jednak nastąpić też przejścia z 0 na 2,3,4 a nie tylko z 0 na 1. Takie przejścia nazywamy: nadtonami Przejście z 0 na 2 będzie więc pierwszym nadtonem, z 0 na 3 drugim, 0 na 4, trzecim i tak dalej. Prawdopodobieństwo maleje wraz z rosnącą liczbą nadtonów.

No dobrze, ale dlaczego patrzymy tylko na 0?, na Pasmo Podstawowe? Czemu nie rozpatrujemy przejść z 1 na 3, 5 na 9 itp? Wszystko rozbija się o prawdopodobieństwo. W temperaturze pokojowej dla większości związków, obsadzone są właśnie pasma zerowe. To na nich jest najwięcej molekuł, stąd prawdopodobieństwo przejścia jest najwyższe. Przez to gdy otrzymujemy widmo, wyższe poziomy są mało intensywne i często nas nie interesują.

Ale zawsze jest jakieś "ale". W przypadku wysokich temperatur, obsadzenie pasm wyższych rośnie. molekuły są tam stabilne, a przez to zdolne do przejść. Można wtedy obserwować przejścia z poziomów 1 na 2, 2 na 3 itp.

To by było na tyle. W kolejnym odcinku, który mam nadzieję pojawi się nieco szybciej niz ten, omówię energię elektronową, bez absorpcji i transmisji czemu poświęcę osobny artykuł.

Źródła:
http://www2.chemia.uj.edu.pl/~zcho/dydaktyka/materia%C5%82y%20spektroskopiaUV%20PDF.pdf
https://chemia.biol-chem.uwb.edu.pl/media/uploads/2015/11/15/spektroskopia-oscylacyjna2015_w_5_6_tAnNLv8.pdf
http://www.fuw.edu.pl/wiki/images/e/e0/Wyklad178-9a.pdf
http://mitr.p.lodz.pl/raman/wiki-2.pdf
https://www.wattpad.com/1116935-energia-oscylacyjna-i-rotacyjna
http://tiger.chem.uw.edu.pl/staff/chalbie/books/16.pdf
http://www.mlyniec.gda.pl/~chemia/ogolna/energia_cz.html