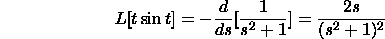The Laplace Transform Method
Prologue to the Laplace Change Technique
The Laplace Change strategy is a procedure for unraveling straight differential
conditions with beginning conditions. It is normally used to unravel electrical circuit
what's more, frameworks issues.
What is a Change Technique?
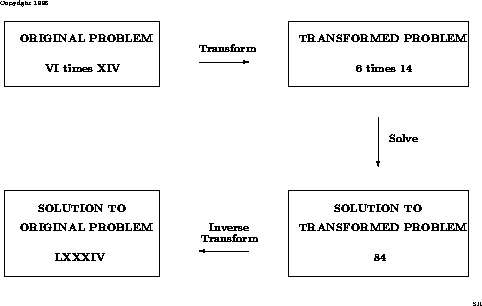
The most straightforward approach to portray a change technique is to think about a case.
Assume we wish to figure the result of VI and XIV, both Roman numerals,
furthermore, express the appropriate response as a Roman numeral. Unless you are a Roman(!), the
to begin with activity is change the Roman numerals to Arabic numerals. VI is 6
what's more, XIV is 14. The changed issue is: process the result of 6 and 14. We
would all be able! The answer for the changed issue is 84. We at that point change over
the arrangement of the changed issue to the answer for unique issue. 84 in
Roman numerals is LXXXIV. This last advance is known as the converse change.
The accompanying chart condenses what we have done.
Why utilize a change technique? A few issues are hard to fathom straightforwardly.
With a change technique, the expectation is that the changed issue is simple
to unravel. That is absolutely the case for the basic case above. One must
likewise consider the trouble of changing the first issue
furthermore, reverse changing the answer for the changed issue.
The Laplace Change Technique for Fathoming ODE
Think about the accompanying differential condition: y'+y=0 with introductory condition
y(0)=3. This is a direct first-arrange differential condition and the correct arrangement
is y(t)=3exp(- t). One needn't bother with a change strategy to take care of this issue!!
Assume we illuminate the tribute utilizing the Laplace Change Strategy. Rather than
illuminating specifically for y(t). We tackle for its accomplice work. We should call it Y(s).
Y(s) is the arrangement of the condition sY(s)- 3+Y(s)=0. We will figure out how to
decide the changed condition later. The key point is that the changed
issue is a Straight Mathematical Issue. We have changed over a direct
differential condition into a straight mathematical issue. It is significantly less demanding to unravel
a straight mathematical issue than a direct differential condition. The answer for the
changed issue is Y(s)=3/(s+1). We should now change Y(s) to a
capacity of t. It will be demonstrated that the capacity of t related with 3/(s+1) is
definitely 3exp(- t).
The Laplace Change of a Capacity
The Laplace Change of a capacity y(t) is characterized by
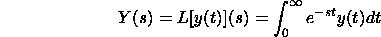
on the off chance that the essential exists. The documentation Ly(t) implies take the Laplace change
of y(t). The capacities y(t) and Y(s) are accomplice capacities. Note that Y(s) is to be sure just an element of s since the positive vital is as for t.
Illustrations
Let y(t)=exp(t). We have
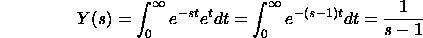
The vital unites if s>1. The capacities exp(t) and 1/(s-1) are accomplice
capacities.
Let y(t)=cos(3t). We have
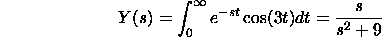
The fundamental meets for s>0. The vital can be processed by doing
joining by parts twice or by looking in a mix table.
Presence of the Laplace Change
On the off chance that y(t) is piecewise consistent for t>=0 and of exponential request, at that point
the Laplace Change exists for a few estimations of s. A capacity y(t) is of
exponential request c if there is exist constants M and T with the end goal that
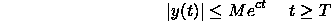
All polynomials, straightforward exponentials (exp(at), where a will be a steady), sine
also, cosine capacities, and results of these capacities are of exponential request.
A case of a capacity not of exponential request is exp(t^2). This capacity
develops too quickly. The basic

does not merge for any estimation of s.
Table of Laplace Changes
The accompanying table records the Laplace Changes for a choice of capacities
.gif)
Principles for Registering Laplace Changes of Capacities
There are a few recipes and properties of the Laplace change which can
significantly streamline count of the Laplace change of capacities. We
outline them beneath. The properties can checked utilizing the basic
recipe for the Laplace Change and can be found in any course book.
Linearity
Like separation and coordination the Laplace change is a direct
task. What does this mean? In words, it implies that the Laplace
change of a consistent circumstances a capacity is the steady circumstances the
Laplace change of the capacity. Furthermore the Laplace change
of an aggregate of capacities is the entirety of the Laplace changes.
Give us a chance to repeat the above in mathspeak. Let Y_1(s) and Y_2(s) signify
the Laplace changes of y_1(t) and y_2(t), separately, and let c_1
be a consistent. Review that Lf(t) signifies the Laplace change of
f(t). We have
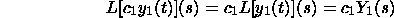
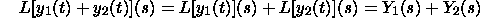
As an end product, we have the third recipe:
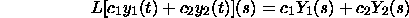.gif)
Here are a few cases:
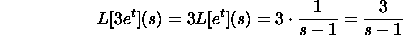
Here we have utilized the outcomes in the table for the Laplace change
of the exponential. Here are two or three more illustrations:
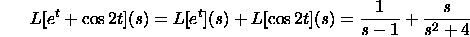
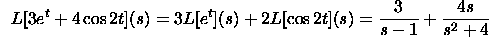
Interpretation Property
The interpretation recipe expresses that Y(s) is the Laplace change of y(t), at that point
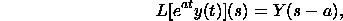
where a will be a steady. Here is a case. The Laplace change of the
y(t)=t is Y(s)=1/s^2. Thus
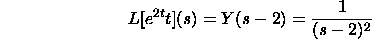
Laplace Change of the Subsidiary
Assume that the Laplace change of y(t) is Y(s). At that point the Laplace
Change of y'(t) is
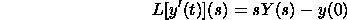
For the second subsidiary we have
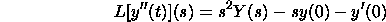
For the n'th subsidiary we have
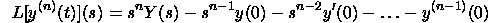
Subsidiaries of the Laplace Change
Give Y(s) a chance to be the Laplace Change of y(t). At that point
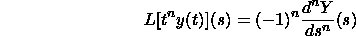
Here is a case. Assume we wish to register the Laplace
change of tsin(t). The Laplace change of sin(t) is 1/(s^2+1).
Henceforth, we have