Zeno's Paradoxes -or- Atomism vs. Continuum

Hey guys, how are you?

Maybe some of you have already heard of some of the famous paradoxes by ancient Greek philosopher Zeno of Elea such as Achilles and the Tortoise (more on that in a second).
Nowadays one might be inclined to consider his works to be simple and ill-informed mathematical problems easily dismantled by modern mathematics.
But, as I want to show you, a closer inspection reveals that Zeno might have provided a much deeper philosophical insight into a dichotomy in science (particularly physics) that has prevailed until today:

The conflict between atomism and continuum

But let me first tell you about the conjunction of two of his paradoxes and then explain to you why they can be interpreted to offer a more refined philosophical perspective than meets the eye.

Zeno's paradoxes

1. Achilles and the Tortoise

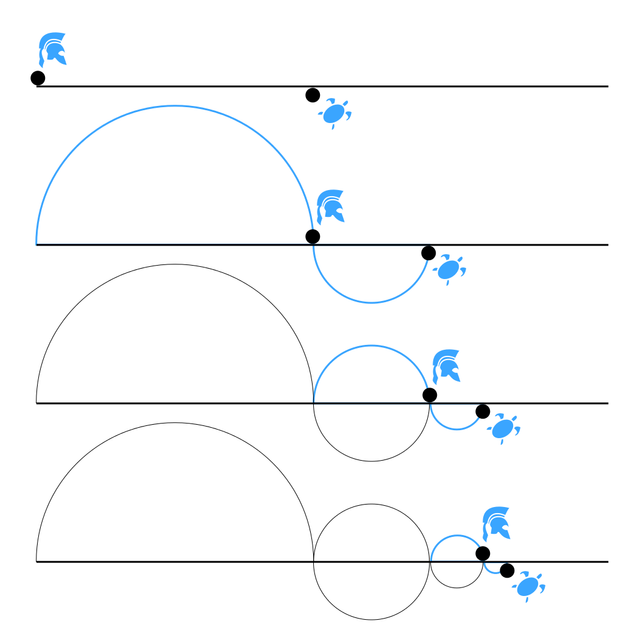
The fastest Greek runner, the hero Achilles, faces a tortoise in a footrace. Achilles runs 10 times as fast as the tortoise but the latter one is given a head start of 100m.
When Achilles has covered those 100 metres the tortoise running at 1/10 of his speed will have covered 10 metres and therefore be 10m ahead of him. As Achilles covers those 10m the tortoise will move by 1m and still be ahead of him.
An iteration of this process ad infinitum shows that Achilles will never reach or overtake the turtle, or doesn't it?

Martin Grandjean, „Zeno Achilles Paradox“, CC BY-SA 4.0

Actually this paradox is easily resolved by noting that the total distance covered by Achilles in this manner -although given by an infinite sum- converges to 100 × 10/9 = 111.1111... , meaning that the tortoise will be reached after a finite distance and time as intuitively expected.
While being taught in every Analysis course nowadays, we have to acknowledge though, that the concept of convergence of infinite sums was unknown to ancient philosophers. But this does not alleviate all the issues reflected in the paradox, a part of its philosophical essence remains intact as we will see.

2. The Arrow Paradox

For any mechanical motion to occur there has to be a time-dependent displacement changing the space occupied by an object like an arrow in flight.
But if we stop time in a duration-less point the arrow "cannot move to where it is not", since no time elapses for it to move there. So any movement is motionless is any instant. But since movement is motionless in any point of time, no movement can occur at all, or can it?

Martin Grandjean, „Zeno Arrow Paradox“, CC BY-SA 4.0

This apparent paradox may also be resolved by current knowledge that was unavailable to its creator. From Theoretical Mechanics we know that any classical movement may be characterized by Lagrangian or Hamiltonian equations in generalized coordinates and velocities/momenta. Even if we stop time in a point the arrow still carries its momentum, causing it to move with elapsing time regardless. You could also argue that movement is just given by the functional dependence of position on time and does not require infinitesimally small movement during duration-less instants.

But how does this relate to atomism vs. continuum conflict?

The debate

Let us thouroughly examine the common theme of both statements.
When you think about it, the fundamental issue brought up by the both of them and giving rise to this historical philosophical debate is the question of infinite divisibility:
Are matter, space or even time constituted by some infinitely divisible and homogeneous continuum or are they quantized by fundamental, indivisible (maybe infinitely small and many) elements called atoms?

In ancient Greece, those opposing schools of thought were most prominently advocated by Aristotle (continuum) and Democritus (atomism) respectively. But for the longest time of recorded histoy Aristotelian physics has been the dominating academic authority in the evolution of science and the Aristotelian continuum was considered a given physical reality. Not until the advent of Cantor's set theory and the dicovery of actual atoms, nucleons and elementary particles did the philosophy of physics return to a duality of both concepts.

Nowadays we are pretty confident that ordinary matter is made of baryons and leptons with the additional hierarchies of quarks constituting nucleons, nucleons and electrons constituting atoms, atoms making up molecules and so forth.
Matter is apparently is not infinitely divisible as far as we know, but consists of aggregations of elementary particles.
But not only have scientist been finding successively smaller elements of matter over the course of history (atoms, nucleons, quarks, ?). The atomistic view begins to degrade altogether when we realize that modern physics describes those elementary particles as nothing more than excitations of corresponding quantum fields on a continuous spacetime.

But at least we know that our spacetime is a continuum, right? Well, even that is not completely understood.
More modern theories like quantum gravity suggest that meaningful physical processes only occur on scales larger than the so-called Planck time t_P≈ 5.4×10^-44s and Planck length l_P≈ 1.6×10^-35m. This means that effectively even our universe might be quantized in units of length and time rather than be be homegeneous on any scale.

Zeno's "foresight"

Zeno's thought experiments are quite visionary in the sense that their conjunction addresses this very duality.

It is believed (sadly there are no known first hand accounts by Zeno himself) that he conceived this paradoxes to argue against both of the atomistic or continuum schools of thought. Presumedly trying to defend his teacher Parmenides' views on eternity, Zeno maybe intentionally, maybe accidentally illustrates that neither philosophy offers a satisfactory description of nature when considered on its own:

Achilles and the tortoise is supposed to demonstrate why space and time can not be a continuum. Zeno shows that infinitely dividing space and time yields a contradiction (not to us but the ancient Greeks). We know that Achilles must be able to overtake the tortoise, therefore infinitely subdividing time/space has to be impossible and there cannot be a continuum.

Similarly, the arrow paradox suggests why time can not be discrete. Since we know there is motion, time can not be constituted by (infinitely many) duration-less instants and nature can not contain indivisible elements.

Although it is fair to assume that Zeno could not have had our modern physical knowledge and both of his paradoxes do not hold up to today's standards I am impressed by the level of wisdom and reflection his teachings reveal upon closer examination.
In particular the seminal comtemplation whether nature is really made up of indivisibles or continua has remained essentially as unresolved as it had been upon its inception.

I hope this has been entertaining and have a nice day! 😉

Sources:

• Zeno's paradoxes
• Aristotle, Physics