用张量积构造正交超立方存在的缺陷
作者 : 贺深泽
设 X 是 n×m 阵列, Y 是 u×v 阵列,它们的张量积(Kronecker product)定义为一个 nu×mv 阵列。
Z=X⊗Y=(xijY|i=1,2,...,n; j=1,2,...m) 即
| x11Y,x12Y,...,x1mY |
| x21Y,x22Y,...,x2mY |
| ...,...,..., |
| xn1Y,xn2Y,...,xnmY |
用这种算法可以从现有较小规模的正交阵列构造出较大规模的正交阵列。这是目前应用最广泛的一种扩展正交矩阵的方法。 但是存在一些问题,如果正交阵列的列向量的水平数多于 3,其张量积的点分布有失均衡性,齐整正交阵列也不能幸免。
设 X 是 n×m 正交阵列,Hk=(hij) 是以“-1”和“1” 为其两个水平的 k 阶 Hadamard 矩阵。 X⊗Hk有 m 块 (x1jH,x2jH,...,xnjH)T,(j=1,2,...,m),
每个块内有 k 列,任何两列构成的点分布图都是 “×”形分布, 其所有试验点都整齐地排列在两条对角线上,参见图 1。
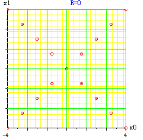
图 1. “×”形分布示意图
Hk⊗X 有 k 块 (h1jX,h2jX,...,hkjX)T, 每个块内 m 列,其中每个列一定与其余(k-1)块每个块中的某一列形成一个“×”。
所有试验设计其试验点分布都应该是充分分散并且是分布均衡的,这是一个基本约定。参见方开泰的论文《均匀设计》,也见《介绍正交超立方试验设计表》。 这种”ד形分布非常不均匀。显然有违均衡性原则。 尽管这些矩阵是正交的,因为太不均匀,不应该包含在正交设计范畴中。它一定会影响效应估计。 如果所研究的过程确实是线性的,问题十分简单,何苦要采用这种设计呢? 如果过程不是线性的,例如是二次曲面或具有二次特征,因为两条平行或交叉直线是二次曲面的母线, 那么“×-”形分布可能会误把曲面判为平面,即把非线性过程判为线性过程。 用线性模型预报非线性过程,是什么结果,可想而知。 如果不在这种 “×-”形分布列上同时安排两个试验因子,那么,任何可能构成 “×-”分布的两个列上只能安排一个因子。 X⊗Hk或 Hk⊗X 都只能安排 m 个因子。换句话说, 尽管一个n×m 正交矩阵与 Hk 的张量积使矩阵规模扩充了 k 倍, 均衡有效的列数仍然是 m 列,不能有效增加研究因子的数目。
例如 Z=W9h5o⊗H4 分 5 个块,每个块内有 4 列。在每个块内,每个列与其他列都构成一幅 “×” 形分布。 图 2 展示了其部分点分布图。 从第一行可以看到属于第一块的 z0-z1,z0-z2,z0-z3 为三个 “×” 形分布。 第二行属于第二块的 z4-z5,z4-z6,z4-z7 为三个 “×” 形分布。 不难归纳, z8-z9,z8-z10,z8-z11; z12-z13,z12-z14,z12-z15; z16-z17,z16-z18,z16-z19 是 9 个 “×” 形分布。 H4⊗W9h5o 分 4 个块,每个块内有 5 列。每个块内的每个列与块内其他 4 列构成的画面正常, 而它与其他每个块中的某一列一定构成一幅 “×” 形分布。 图 3 展示了 Z=H4⊗W9h5o 的部分点分布图。(这些图形由我自己的程序制作。) 第一行中,0-z5,z0-z10,z0-z15 为三个 “×” 形分布。 第二行中,z1-z6,z1-z11,z1-z16 为三个 “×” 形分布。 不难归纳,z2-z7,z2-z12,z2-z17; z3-z8,z3-z13,z3-z18; z4-z9,z4-z14,z4-z19 是 9 个 “×”形分布。
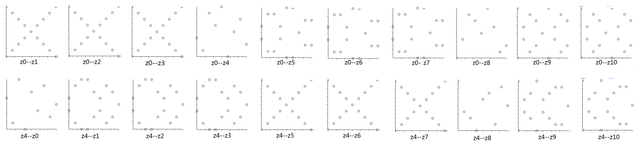
图 2. W9h5o⊗H4 的点阵图(部分)
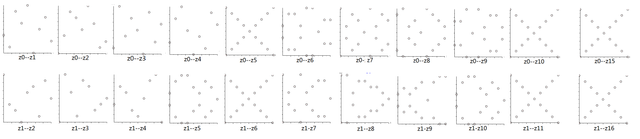
图 3. H4⊗W9h5o 的点阵图(部分)
结论是显然的, 虽然 H4 把 W9h5o 扩大了 4 倍,有 20 正交列,但实际上只能研究 5 个因子。 如果把 H 换成其他 u×v (v<u) 二水平正交阵列,上述讨论依然有效,对于齐整正交阵列同样有效。
要看明白这一点,必须显示出张量积的结果的点阵图,必须有相应的察看程序。从相关矩阵是不能看出来的。
为了看得更清楚,我们取 OHC16h6o 的两个正交列和一个 H4 的两列的张量积。 张量积的结果是 2×2=4 列。向量自己与自己的图形一定是直线,予以省略, 其余二维点阵图具有对称性。四个列构成的二维点阵图见图 4. 假如在前两列上安排两个因子。由于前两列为“×” 形分布,只能安排一个,不失一般性, 可以安排在第一列(编号 x0),第二列(编号 x1)不能再安排因子。 假如在第三列(编号 x2)上安排一个因子,因第三列与第四列为“×” 形分布,第四列(编号 x3)不能再安排因子。 总共只能安排两个因子。实验设计方案:只能是以下四种之一。
- x0,x2;
- x0,x3;
- x1,x2;
- x1,x3;

图 4. W16h2o⊗W4h2o 分别正交化后张量积的二维点阵图集
两个多水平正交阵列的张量积有新定义域,其边际分布不是均匀的,其点分布中心密集而周边稀疏。 例如 W7h3o⊗W9h5o 的定义域为 (-12,-9,-8,-6,-4,-3,-2,-1,0,1,2,3,4,6,8,9,12), 不能均匀地划分定义区间,违背了超立方的定义。其典型分布见图 5。
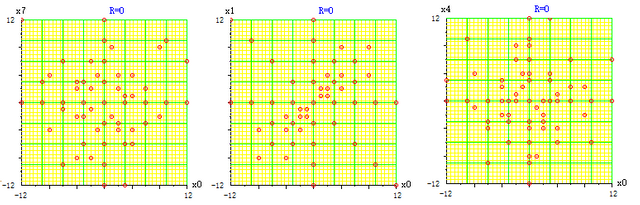
图 5. W9h5o⊗W7h3o 的典型点阵图.
D.Bingham, R.R.Sitter, and B. Tang (2009) 对这种状况提出了改进方案。将张量积中各列的阵列 Y 的行列进行随机性交换加以改造,使各列的 Y 不同。 这样的改造思想是可取的。但他们的所谓随机的行列交换是同构变换。同构变换表面上看起来改善了点阵排列, 本质上不改变什么。因此,应该选用一组 m 个非同构的正交阵列,而且第一列也应该是随机的。 这就必须事先准备好足够多不同构的同规模正交阵列。这不是一件容易的事。
参考
[1]. D.Bingham, R.R.Sitter, and B. Tang, Orthogonal and nearly orthogonal designs for computer experiments. Biometrika 96 51–65, (2009)