Xinta's music lessons: Lesson 2

xinta (55)in #music • 7 years ago (edited)

In the previous lesson we've learnt that a sound can be decomposed into several sinusoids; mathematically they could be an infinite number.

These sinusoids are called harmonics when their frequency is an integer multiple of a fundamental frequency, which is the one that makes us perceive the sound as having a specific pitch (and it's the lowest frequency). It isn't that easy for every sounds, though, because sounds can be produced in such a way that their “recipe” doesn't contain only harmonic frequencies; it's the case of e.g. unpitched percussion instruments, for which we talk of indefinite pitch.

The fundamental frequency is also the stronger frequency: the amplitude of all the other waves is lower. For the “recipe”, it doesn't matter the absolute value of the amplitudes of the partials, but their strength relative to each other.

Our ears, being incredible, yet limited and not perfect sensors, have their say in our ability to perceive sounds' frequencies. In particular our ears can't perceive sounds with a frequency lower than 20 Hz circa, nor sounds with a frequency higher than 20,000 Hz circa. The exact values are subjective and depend also on factors like age, or past life habits. Each individual, indeed, has its own frequency and loudness response, which is a function of frequency.

As you can imagine, we aren't able to grasp all the harmonics of a sound. (But it doesn't mean they haven't physical effects which can impact on us — for example frequencies lower than 20 Hz could be anyway felt bodily.)

Dissonance and consonance

We might explain harmony rules through, well, harmonics.

When you combine two sounds, they can play “well” (they are someway consonant) or “badly” (they are someway dissonant) together.

Warning: consonance and dissonance are more like cultural subjective concepts than objective universal description. As an intuitive device, I'm using the idea of coincidence of partials.

Intuitively, two sounds play well together (they form a consonance) if their harmonics overlap “well”. Consider a sound with a fundamental frequency of 440 Hz, i.e. with a pitch of 440 Hz. Its second harmonic is 880 Hz (2×440 Hz), so if we play a sound with pitch 880 Hz, we expect that it mingles particularly well with the former.

The interval considered (when the ratio between two pitches is 1:2, or 2:1) is called an octave, and it's traditionally and solidly considered a consonant interval: those two sounds play “well” together.

Too well, indeed: they play so well that some people could say they are the same “note”, the same sound, despite the fact that one is higher! This makes sense if you think about the second harmonics. And it is also important because it can explain another thing we need to assume: the number of notes is finite (frequencies are not…), and we can call with the same name pitches having frequencies whose ratio is a power of 2. (That is, if f is the frequency of a note, 2f, 4f, 8f, 16f… but also, of course, f/2, f/4, f/8 and so on, provided the frequency stays in the range of audible frequency.)

We'll see that interesting harmony is made of “tension”, and this is given by dissonance. Music made only with notes in octave would be rather boring. It wouldn't be different from playing a melody alone.

Other intervals are dissonant, or just less consonant; it seems so for instance if you combine sounds whose harmonics doesn't “mix well”, e.g. pitch 440 Hz and 770 Hz; you see that the second harmonic of the first sound is near the first harmonic of the second sound, but it isn't enough near.

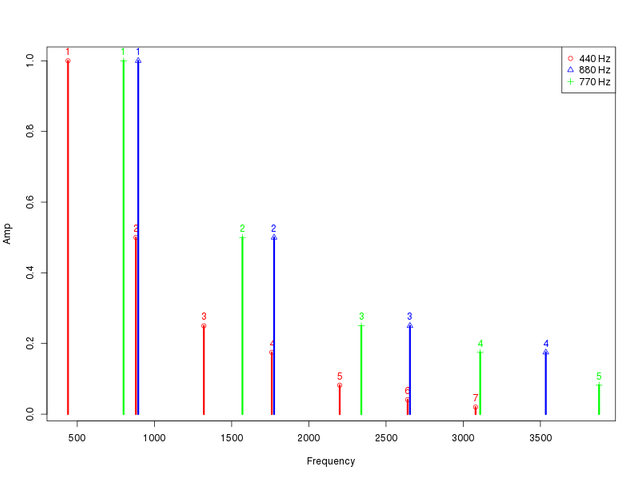
In the image I've shifted a little bit frequencies that are the same in order to avoid graphical overlapping. You can see that harmonics of the pitch 440 Hz (red) and 880 Hz (blue) overlaps, while the first (and only, in this case) overlapping between 440 Hz (red) and 770 Hz (green) happens between harmonics seventh (which is rather weak in this example) and fourth.

Tuning and the twelve-tone equal temperament

Fretless string instruments can produce different continuos pitches easily. Think about a string of a violin: when the bow makes it vibrate, it produces a note at specific pitch, depending on its tension, thickness, and length. While playing, you change the length pushing the string on the fingerboard, and since there aren't frets, you can change that length continuosly, and the pitch will follow.

The thicker a string is, the lower the pitch it emits; the longer a string is, the lower the pitch it emits; the more stretched a string is, the higher the pitch it emits. Conversely, the thinner a string is, the higher the pitch it emits; the shorter a string is, the higher the pitch it emits; the less stretched a string is, the lower the pitch it emits.

All this explains why the strings of a violin (or other similar instruments), even if they are all the same length, have different thickness and are set to different tensions. You modify the tension by rotating a peg, but this is left for the tuning and you don't do it while playing.

Now, let's consider a single string.

Thickness is a mechanical property of the string and as already said it can't be changed. The maximum length too, can't be changed: the string was made with that length. Indeed the actual length doesn't matter: when I say length, I refer to the length of the segment of the string between two fixed nodes; the segment between these nodes is the segment you excite (pluck or bow, for instance) and that vibrates.

So the length of a string of a violin (or other string instruments) is determined by the distance between the peg, where one end of the string is pinned to (and rolled around), and the bridge, where the string “rests” (and then it is fastened to the tailpiece — violins and similar instruments — or bridge pins — guitars). These two “nodes” determine the sounding length of the free string, i.e. when you don't peg it on the fingerboard with your finger.

More about string vibration; the details are beyond the scope of these lessons.

Now you can play a melody you have heard yesterday at the radio, and it will sound good to you. (Unless you're one of those rare persons having the absolute pitch).

But, are you playing those exact notes of the melody as you heard it? It hasn't to be so: the very important thing in a melody is the relationship between notes, the “jumps” the melody does. The only interval I've talked about so far is the octave. The other obvious interval is the unison: the note stays the same.

Let's stick with these two: imagine a melody made of four notes and two pitches, pitch “A” and pitch “B”, where pitch “B” has a frequency which is 2 times the frequency of “A”. That is, “B” is “A” one octave above (given that your single string play “A”, you obtain ”B” halving the length of the string, so you'll put your finger in the middle). Our melody is A B B A, played with a certain rhythm. Play it for a friend of yours. Now rotate the peg so to diminish the tension of the string. Play again your melody. Is it the same? Even if the pitches aren't exactly the same, you are able to recognize your melody. You are just playing it in a different tuning, but it is that very melody.

You can try also with a more complex melody you've obtained pressing the string not just in the middle. The result will be the same: you can reproduce the same melody even if you rotate the peg so that the frequencies of the notes you're playing are lower or higher. But the relationships among the notes of your melody will be the same.

Now you meet a friend who has a guitar with just one string, as your violin, and you want to play the melody altogether. Let us suppose that your melody's first note is the lowest note your single string can play. Your friend will try to play that first note on his single string guitar. He must rotate the tuning peg to raise or lower the pitch of his string, until it sounds the same as the one of your string. The result will be this: both strings produce a note with the same pitch.

Good! Now you teach your friend your melody. Your friend trusts his ears and try to imitate what he's listening to. But he could realize that you did a very strange melody and that he isn't able to reproduce it because few notes will always be out of tune. Why?

This is because guitar has frets and so a guitarist can't produce every frequency between the lowest and highest possible for a string. They can produce only specific pitches, decided by the way the frets are put.

Something similar is true also for other instruments, for example pianos. They can produce notes, but the pitches are predetermined by the tuning.

In a piano it is also evident another thing (which is not evident in a guitar): there's a repeating “pattern”. If the piano is correctly tuned (i.e. tuned as we expect it to be according to our common musical culture), you well see that the right key (marked “R”) in the picture produces a sound which has double the frequency of the one produced by the left key (marked “L”).

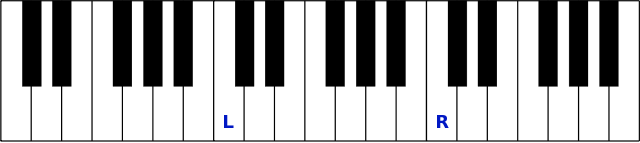
(Image credit, slightly modified according to the remix permission of the CC license.)

The same is true for the keys on their right, and so on. The notes between the “L” (included) and the “R” (excluded) are all the notes modern western music considers inside an octave; they are 12 (count both white and black keys).

In fact players of different instruments must agree on the frequencies that notes have, and before this we also need to agree on how many notes there are. This makes possible the existence of an orchestra with several instruments that use different ways to produce sounds. This makes possible for a piano (tuned) to play in an orchestra, and to improvise an accompaniment for the melody the violin is playing, provided the latter sticks to the rules: a violin isn't constrained to a specific number of notes with “fixed” frequencies.

The division of the octave into 12 notes, and their relative frequencies, are choices explained by history (especially of few musical instruments like piano and harpsichord) and culture.

These choices are called commonly equal temperament, but more exactly twelve-tone equal temperament. In these lessons I will assume the 12-tone equal temperament.

About ratio among notes (hence tuning) just intonation would be more natural, but would exclude the use of instruments like a piano.

In order to allow our instruments to play well altogether in an orchestra, we must tune them in the same way, and we've just seen the equal temperament solves every problem (almost). But indeed it doesn't fix frequencies; briefly it just says that, if a certain note has the frequency f, then the note one semitone higher would have frequency 2^1/12f (if you've read my article about Exponentiation, you know that 2^1/12 is the twelfth root of 2).

This is why a frequency of a specific note is decided beforehand. Many readers likely will know about the 440 Hz, for which they sell also tuning forks which vibrate at that frequency and haven't (almost) any harmonics beyond the first; that is, it is almost a pure sinusoids with a frequency of 440 Hz.

Once you have decided the frequency of a specific note, the other notes' frequencies will be a conseguence of this choice. The tuning with the A (the name of a specific note according to English notation) at 440 Hz is common and standardized, but other choices are used; for example 441, 442 Hz, and 443 Hz.

Writing the notes

Now we know that, as far as we are concerned, they exists 12 notes in an octave. These notes have names, which may be different according to the language. Even if the names are different between English and, say, Italian, the notes are the same, according the standard I've talked about above.

Writing notes is a matter of notation: how could we describe to others our song? Or just the fact that a player should play a specific note for a certain amount of time? Music-as-we-know-it has a well established set of rules to transcribe on paper notes, durations, rhythms and other things. It's a language, a language through which we say what should be played and you also can suggest how.

Anyway interpretation is what makes it real. Using the analogy of a human language like English, think about how a text like this is written and how different readers might speak it out loud differently.

Remember also that English isn't the only language; in analogy, other notations may exist; special notations for strange music can be invented to better transmit the ideas to the future performers.

The names of the notes and their octave

When I need to call a notes, in these lessons I'll use the so called anglosaxon (English) notation.

We have said that according to 12-tones equal temperament the notes are 12; there are seven natural notes (the white keys on a piano) and five altered notes (the black keys on a piano).

The seven notes and the five altered notes are (from lower pitch to higher pitch): C, C#, D, D#, E, F, F#, G, G#, A (we've met this one talking about tuning), A#, B. The # is the sharp symbol, more correctly in text we should use ♯, but # is a fair approximation. The sharp symbol raises the pitch of the note of a semitone, that is half of a tone; in equal temperament we obtain the frequency of A# (for instance) by multiplying the frequency of A by 2^1/12.

The altered notes are also Db, Eb, Gb, Ab, Bb, where b is a fair typographic approximation of the flat symbol, ♭. The flat symbol lowers the pitch of the note of a semitone. In the equal temperament they are different names for the same pitch: C# = Db, D# = Eb, F# = Gb, G# = Ab, A# = Bb. There are a reasons why you would like to call them differently. We'll see it in a future lesson.

German notation is very similar, but B stands for English Bb, and unaltered B is H. Other notations exist. I think that the second most used notes' names are: do, do# = reb, re, re# = mib, mi, fa, fa# = solb, sol, sol# = lab, la, la# = sib, si. Again, # is the sharp symbol ♯, and b stands for the flat symbol ♭. This one is the convention used in Italy.

If you raise of a semitone the last B in the scale, you obtain again a C, but one octave higher with respect to the one you started from. So, we haven't a single C, but several C, one for each octaves. All these C altogether makes a pitch class. The same works for the other notes.

If we call the middle C as C4 (where the number specifies the octave in a conventional way called scientific pitch notation), the C of the next octave is C5, and the ratio between their frequency, freq(C5)/freq(C4), is 2.

Raising a note of a semitone means (in 12-tones equal temperament) to multiply its frequency f by 2^1/12, as already said. If you do it 12 times, i.e. 2^1/12×2^1/12× … ×2^1/12 12 times, i.e. (2^1/12)¹², you obtain 2f, that is, the same note but an octave higher, which is what we expect because we've devided the octave into 12 different pitches.

Writing notes: the staff

Other names for the staff are stave and pentagram. It's made of five parallel lines. A note's head (a circle) can be on a line, or between two lines. You can imagine that they exist invisible lines above the last upper line, and below the first bottom line. This way you can continue to write notes, though going too much up or too much down would make the score less readable.

Without any other indicators, the note you can write on the staff are the seven natural notes.

But… how is it possible to write all the possible notes of several pitch classes this way? And which notes are those?

We need clefs. Clefs say which note stays on a specific line; the others come as conseguence. In this rather long lesson I show you only the violin clef, also called the treble clef, and the bass clef. These two clefs are the most used, especially in pop music (where likely they are the only one used).

The treble clef tells where the G belonging to a specific octave (G4 according to the scientific pitch notation) is, and it is put so that it suggests the second line (counting from bottom).

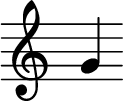
Follow the curl of the symbol: it rests on the second line! So the note you see is a G4. (G4 is a whole tone below A4, which is usually 440 Hz; so its frequency is 440 / (2^2/12) = 391.9954 Hz)

The bass clef tells where the F3 is:

The dots “embrace” the line where the F3 is.

These two clefs are chosen so that if you stack two staves one over another, the lower (of course…) with the bass clef and the higher (of course, again…) with the treble clef, you can imagine an eleventh line in common between them, being it the line where you write the C4, the middle C, the C that is at the center of a piano; and in fact piano scores use two staves, one with treble clef and another with bass clef — by default, but of course specific pieces can change this according to their needs.

In fact a notational fact is that you can change the clef wherever you need, if you think it makes easier to read the music.