📈 True Profitable Cryptocurrency Trading 💰 - [RESEARCH PT 5.]

I’m still doing my research into cryptocurrencies, it’s been like 1 month now or actually more, and I have made some good progress, there is a lot to be learned about the market and how it moves. I think I am getting to the end now, especially since that the current strategy seems pretty solid.
So I haven’t talked much about cryptocurrencies for this reason, I don’t want to spoil things, but when I will talk about cryptos again, I will do it based on my methods now. I think I have successfully quantified a lot of stuff about cryptocurrencies, so I might even be able to start a forecasting service in the future.
Transformations
In this article I just want to talk about transformations and the importance of it. I have been using LOG based transformations of the error numbers for example, and there are more like this, but can also be applied to the price itself to smoothen things out.
In some cases using the raw value is better, but in other cases we just want a relativistic ratio, and for that LOG comparisons are very useful.
Now the LOG ratio can also be used on itself with 1 argument, which will result in mapping out the disordered price data on the LOG curve, thus smoothening it out and removing the exponential element from it, as the LOG curve is in exponential space, obviously the exponential element will be removed or sort of squashed out.
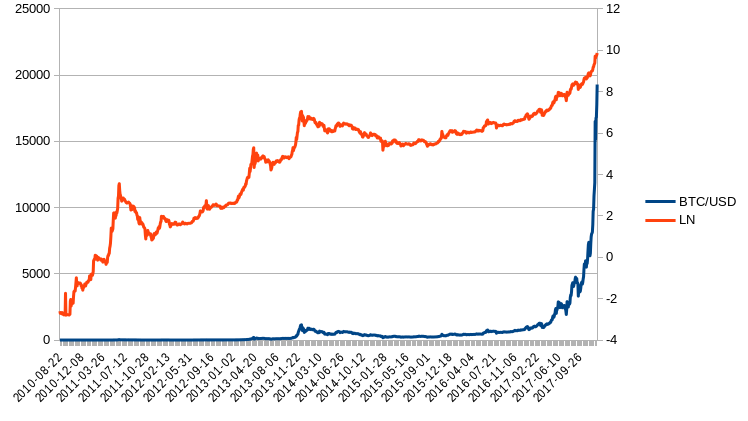
LOG Transformation
I like to use the natural logarithm, it’s actually irrelevant since any base achieves the same effect, but I just like the LN more. Now with bases larger than 10 the output usually becomes more smooth, but unless it’s a very exponential data to begin with, it doesn’t really matter. With huge bases, the data might converge towards a straight line with very small decimal differences.
| Appearance | Function | Inverse Function |
|---|---|---|
| In Spreadsheet | LN(x) | EXP(x) |
| Math notation | log e (x) | ex |
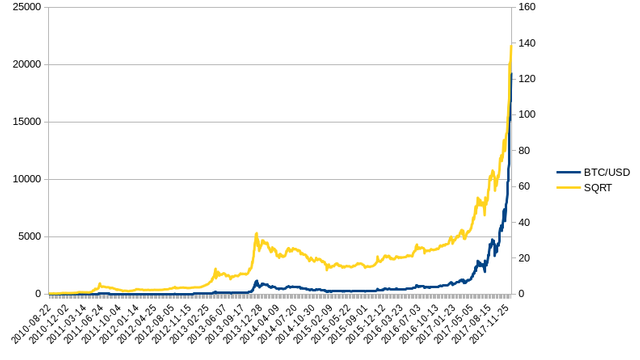
Root Transformation
Another basic transformation function is to take the root of the series, which simply might be the square root or higher level root. Again it doesn’t matter since the relationship remains the same, but as you increase the root number the series becomes smoother and could become a straight line.
| Appearance | Function | Inverse Function |
|---|---|---|
| Math notation | x(1/2) | x2 |
Others
Of course there are other transformation methods, more sophisticated, but with these you can already make the price more smooth for whatever reason, and transform them back after you are done with the analysis. So you could perhaps plot some tools on the transformed price and then transform back the outputs into the real price.
If you increase the parameter then the price converges towards a straight smooth line, so that may indicate the price or the trend better for whatever reason you might want to use it for.
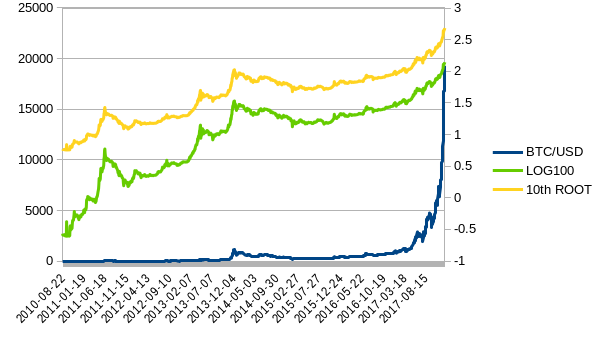
So a more smoother transformed price with a clear trend indication could be very helpful, now obviously this could be customized, with more advanced transformation techniques we can quantify the changes much better, but as basic tools you could use these to help you analyze the price better.
I use the LN function almost everywhere, it’s very useful. I hope this information helps your market analysis become more accurate!
