Modeling and Analysis of Bitcoin Volatility Based on ARMA-EGARCH Model (8)
In [31]:
compare_ARCH_X = pd.DataFrame()
compare_ARCH_X['Model'] = ['ARCH','GARCH','EGARCH']
compare_ARCH_X['RMSE'] = [get_rmse(kline_test['realized_volatility_1_hour'][280:320],kline_test['recursive_ARCH'][280:320]),
get_rmse(kline_test['realized_volatility_1_hour'][280:320],kline_test['recursive_GARCH'][280:320]),
get_rmse(kline_test['realized_volatility_1_hour'][280:320],kline_test['recursive_EGARCH'][280:320])]
compare_ARCH_X['MAPE'] = [get_mape(kline_test['realized_volatility_1_hour'][280:320],kline_test['recursive_ARCH'][280:320]),
get_mape(kline_test['realized_volatility_1_hour'][280:320],kline_test['recursive_GARCH'][280:320]),
get_mape(kline_test['realized_volatility_1_hour'][280:320],kline_test['recursive_EGARCH'][280:320])]
compare_ARCH_X['MASE'] = [get_mape(kline_test['realized_volatility_1_hour'][280:320],kline_test['recursive_ARCH'][280:320]),
get_mape(kline_test['realized_volatility_1_hour'][280:320],kline_test['recursive_GARCH'][280:320]),
get_mape(kline_test['realized_volatility_1_hour'][280:320],kline_test['recursive_EGARCH'][280:320])]
compare_ARCH_X
Out[31]:
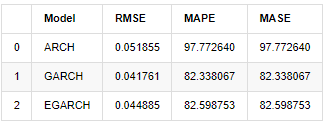
In terms of indicators, GARCH and EGARCH have some improvement compared with ARCH, but the difference is not particularly obvious. After multi sample interval selection and verification, EGARCH will have better performance, which is mainly because EGARCH explains the heteroscedasticity of samples well.
- Conclusion
From the above simple analysis, it can be found that the logarithmic return rate of Bitcoin does not conform to the normal distribution, which is characterized by thick fat tails, and the volatility has aggregation and leverage effect, while showing obvious conditional heterogeneity.
In the prediction and evaluation of logarithmic rate of return, the ARMA model's intra sample static prediction ability is better than the dynamic one significantly, which shows that the rolling method is obviously better than the iterative method, and can avoid the problems of overmatching and error amplification. The rate of return outside the sample is difficult to predict, which satisfies the weak efficiency assumption of the market.
In addition, when dealing with the thick tail phenomenon of Bitcoin, that is, the thick tail distribution of returns, it is found that the GED (generalized error) distribution is better than the t distribution and normal distribution significantly, which can improve the measurement accuracy of tail risk. At the same time, EGARCH has more advantages in predicting long-term volatility, which well explains the heteroscedasticity of the sample. The symmetric estimation coefficient in the model matching is less than the confidence interval, which indicates that there is a significant "asymmetry" in the return rates fluctuation of Bitcoin.
The whole modeling process is full of various bold assumptions, and there is no consistency identification depending on validity, so we can only verify some phenomena carefully. History can only support the probability of predicting the future in statistics, but the accuracy and cost performance ratio still have a long hard journey to go.
Compared with traditional markets, the availability of high-frequency data of Bitcoin is easier. The "realized" measurement of various indicators based on high-frequency data becomes simple and important. If nonparametric measures can provide quick observation for the market that has occurred, and measures with parameters can improve the input accuracy of the model, then taking the realized nonparametric measures as the "Hyperparameters" of the model may establish a more "complete" model.
However, the above is limited to theory. Higher frequency data can indeed provide more accurate analysis of traders' behavior. It can not only provide more reliable tests for financial theoretical models, but also provide more abundant decision-making information for traders, even support the prediction of information flow and capital flow, and assist in designing more precise quantitative trading strategies. However, the Bitcoin market is so volatile that too long historical data can not match effective decision-making information, so high-frequency data will certainly bring greater market advantages to investors of digital currency.
Finally, if you think the above content helpful, you can also offer a little BTC to buy me a cup of Cola. But I don't need coffee, I will fall asleep after drinking it···