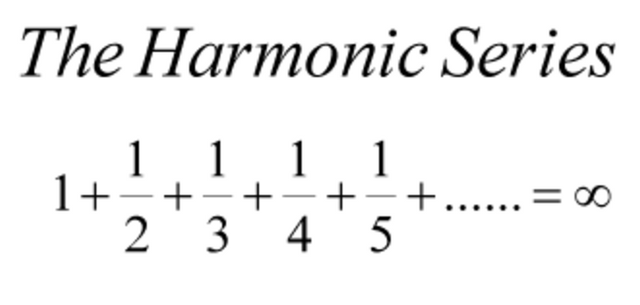
The Harmonic Series - How is it possible that adding a series of numbers that tends towards zero sums to infinity?

One of the reasons I love mathematics so much is it can simultaneously build up a strong set of convictions and intuitions. And just when you believe you have it all figured out, an interesting problem or paradox can come along that challenges everything you thought made logical sense.

Enter the Harmonic Series

The Harmonic Series, is expressed mathematically as the infinite series of fractions that follow the given pattern:

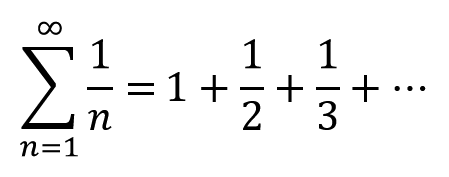
You might recognize the term harmonic from music. And you would be correct. Consider the following:

When a string, for example the low low C on a piano, vibrates, it oscillates up and down over the length of the string. The wavelength of this frequency then is twice the length of the string, since it takes a full excursion back and forth to begin to create the air oscillations that our ears perceive as sound.

The wavelength of a string's frequency then is 2L, or twice the length of the string. (Source)

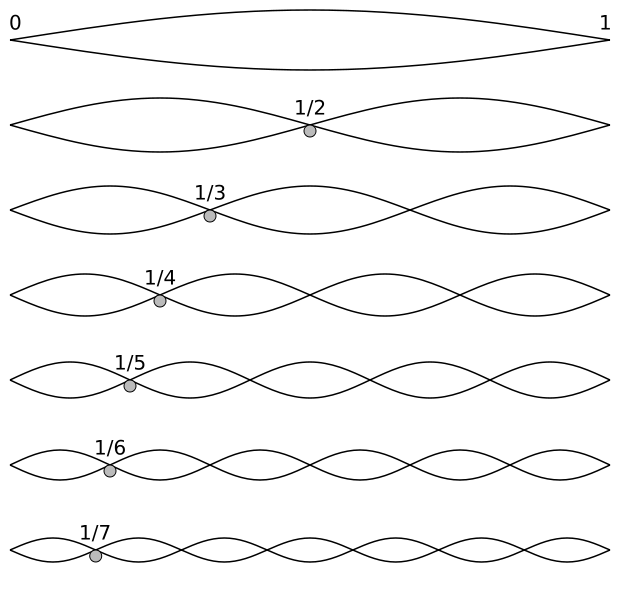
This means that whenever you play a string on an instrument, it will vibrate at its full length and at any integer divisions of the string. These correspond with pitches that we perceive as sound. Below is the harmonic series represented musically for "Middle C":

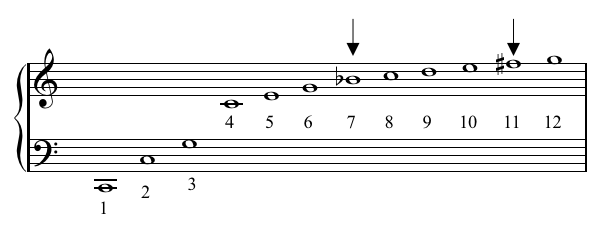
So the idea of this sequence is rooted in music theory. When you get to the mathematical theory behind it, it's even better!

When I first learned about series and infinite sums, I was completely floored by the concept. It is possible to take an infinite sum and have a finite upper bound for its result.

Take, for instance, the following infinite sum:

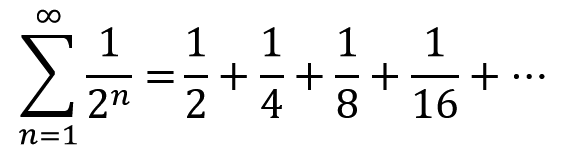
If you logically work your way through this, the terms of the series are tending to zero. Every time, we are adding a negligible amount to the overall sum. While we are stacking up items to infinity, the overall stack of items is not rising out of control.

How do we know this? We could look at partial sums of terms. These are sums of the first 2 terms, 3 terms, 4 terms, and so forth. If that pattern has a limit, the overall sum should also have a limit.

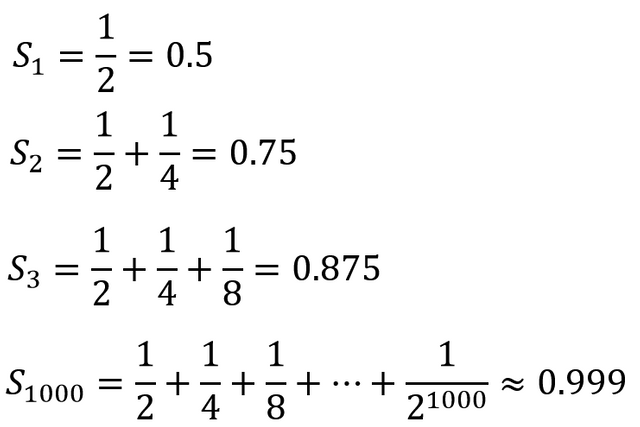
For this particular sum, this can also be explained with a unit square. If you continue to half a 1 x 1unit square (Area = 1) to infinity, when you sum up the individual parts, their upper bound should be 1, even though the process of halving would continue forever.

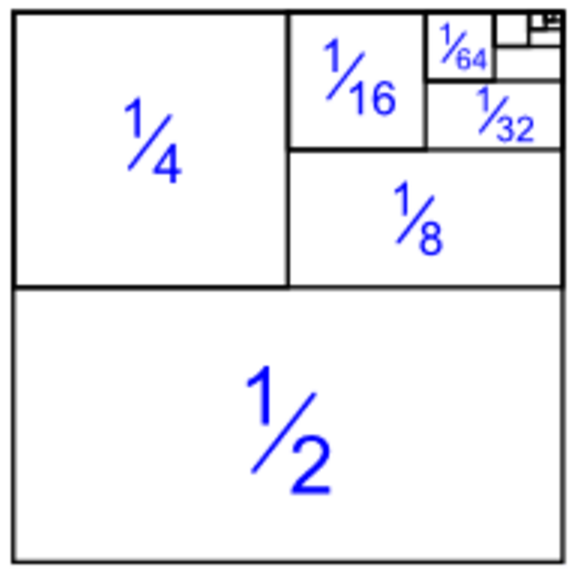
This all makes intuitive sense. That is, of course, until you get to the Harmonic Series.

If you are to sum the series of fractions 1 + (1/2) + (1/3) + ... to infinity, despite the fact the terms are decreasing towards zero, the entire sum tends to infinity.

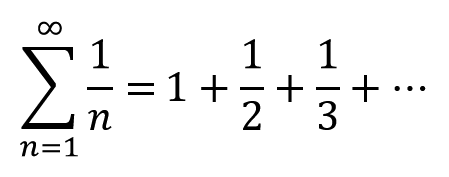
From an intuitive sense, the fact the terms are decreasing to zero means that eventually you are adding negligible amounts every time. So, why is it these negligible amounts make the entire sum tend to infinity?

They are not moving to zero fast enough

Consider partial sums. Last time with a sum that had a bound, these sums tended to something. This time, we aren't getting the same behavior:

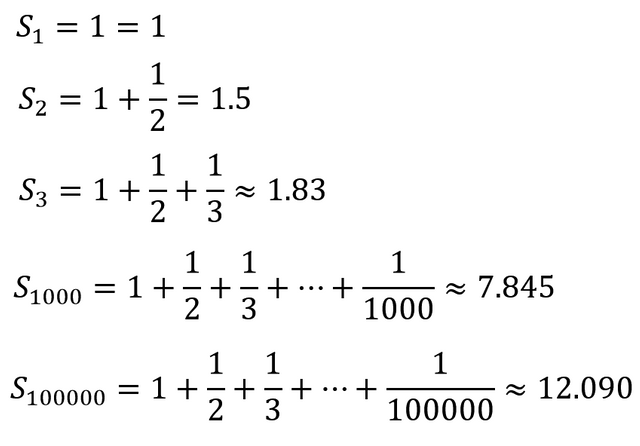
So, informally, this sequence of partial sums has no limit. This should mean the entire series has no limit and diverges to infinity.

More formally, something like this is really happening.

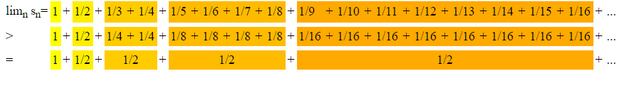
This image above is from the following site with a sobering reality if you were to try to brute force compute further partial sums of the harmonic series:

The harmonic series diverges - but so slowly, that a numerical experiment does not show that. Even if a machine would have been adding terms at a rate of 10-9 seconds and would have started 15 billion years ago, (about 1017 seconds), the value of the sum would still be about Log(1026) which is less then 60. (Source)

Therefore, without partial sums, this image demonstrates that if you replace successive terms of the harmonic series with terms that are less, you will get a comparable infinite sum of 1/2.

Intuitively, if one sums up 1/2 an infinite amount of times, it would not have a limiting value. But, the harmonic series is a series of terms even greater than this summation. So, by comparison it is greater than something that has no limit, so it too must have no limit.

---

Proofs with Calculus

Calculus. Nice, friendly calculus. With it, and comparison testing, we have a really awesome way to actually prove this sum diverges.

Take, for instance, a geometric representation of the harmonic series as follows:

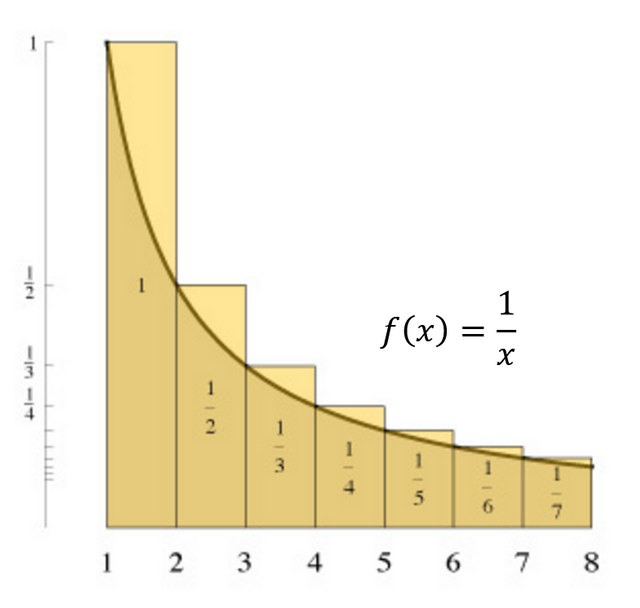
Every bar on this chart represents a rectangle with a height of each term of the harmonic series, with every width being 1. Geometrically, the area of each bar represents each term of the harmonic series. Superimposed on the same graph is f(x) = 1/x. This is a continuous function, that is only shown on the interval [1, ∞). For those that have taken calculus before, you will recognize these bars as a left hand Riemann Sum that is to approximate the area under the curve.

Notice how all of the bars on this graph are over the curve f(x) = 1/x. This means the combined area of the bars all together must be strictly greater than the area contained between the curve 1/x and the x-axis. Thankfully, calculus gives us a way to calculate this area using improper integration:

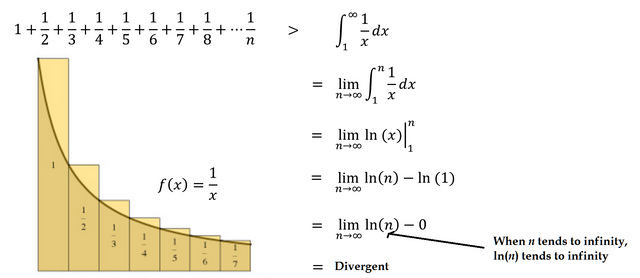
Because the integral diverges to infinity, the sum of our rectangles must also diverge to infinity.

The slickest proof I've ever seen - it only involves intuition and a counterexample.

The following proof comes to us from Leo Goldmahker from the University of Toronto. It is SUPER straightforward to understand because it involves a counterexample to start.

Suppose the harmonic series DOES have a finite sum, H. If it does, it can be proven that the sum has another equivalent sum that is in terms of itself plus 1/2. Of course, this is nonsense, and our original assumption of a finite sum must be rejected.

---

The Alternating Harmonic Series

In the irony of ironies, if you decide to alternate every term of the harmonic series from positive to negative, the series actually converges. In fact, it famously converges to ln(2).

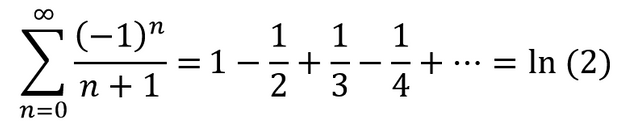
Why exactly? The quick answer is that when we flip every other term to a negative value, it helps the entirety of the sum get to zero faster. This gives it more of a fighting chance to have a convergent value.

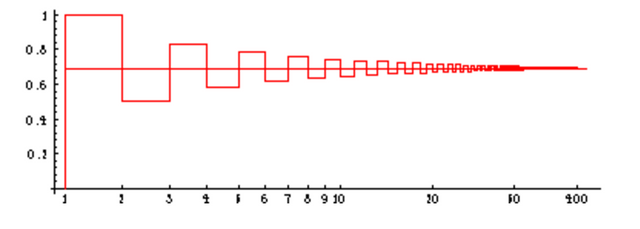
It can also be easy to tell with partial sums why this is occurring. Below is a graph of the first 400 partial sums of the series. In it, it is fairly easy to tell a limiting value of around 0.7, approximately the value of ln(2).

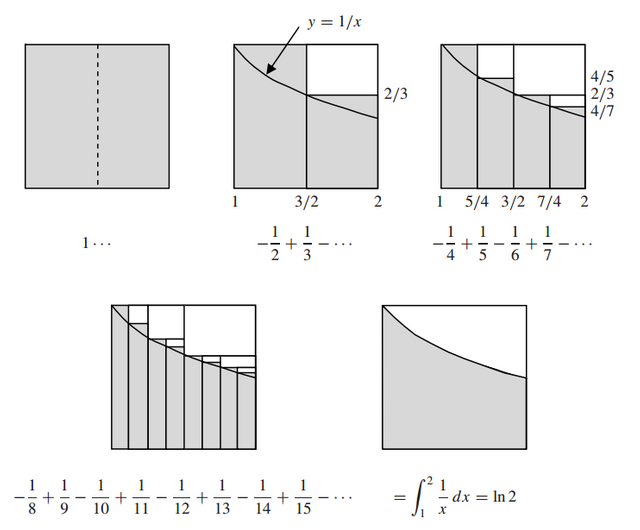
The proof of why exactly the sum converges to ln(2) can get fairly heavy, so I prefer the visual approach. The following is my favorite demonstration of this fact, and it comes to us from Matt Hudelson at Washington State University.

In this, he starts off with a unit square and partitions bits of it away to form a pattern of the alternating harmonic series. This visual shows a limiting value that converges to ln(2).

---

When it comes to the infinite, I have learned one incontrovertible fact throughout my studies:

Whatever I think is happening most likely is not.

I am absolutely fascinated with infinities and the intuitive and sometimes counterintuitive ideas that can be explored. And, this topic is just the tip of the iceberg. But, in positive news, it does remind me to consistently expect that no matter how much I think I know about the world, there is always more to learn.

That is the true beauty of mathematics that keeps me coming back for more!

---

Sources:

1. Music Pictures - Earlham College
2. Partial Sums to (1/2) - Mathematik
3. Confused GIF - Giphy

---