The ASS Postulate for Triangle Congruency and Why it Doesn't Work

If you ever sat through an average high school geometry class, at one point you inevitably learned about ASS.
And SSS. And SAS. And...just oh so many acronyms for triangle congruency postulates....
And, if you mindlessly went through your Geometry classes, you probably just learned to memorize such acronyms and never really think much about them again.
It's actually pretty funny though how information like this just sticks. When I casually drop the "I'm a math teacher" in conversations with people, its uncanny how many people come back to acronyms like these they learned in their math classes along the way. And, almost everyone that recalls these usually had an experience with a math teacher that made some terrible joke about how ASS doesn't work.
But, almost no one I talk to ever remembers why.
And it really is a shame, because when taught properly, the reason "it" doesn't "work" is painfully obvious.
You see, all of the acronyms for triangle congruencies usually assume you are asking the following question:
What is the absolute minimum amount of information I need to know about one triangle to construct another triangle that is identical.
For example, consider the case of SSS, or "Side Side Side". This postulate assumes that if, at minimum, I know the lengths of three sides of one triangle I can make an 👏exact👏carbon 👏copy of it.
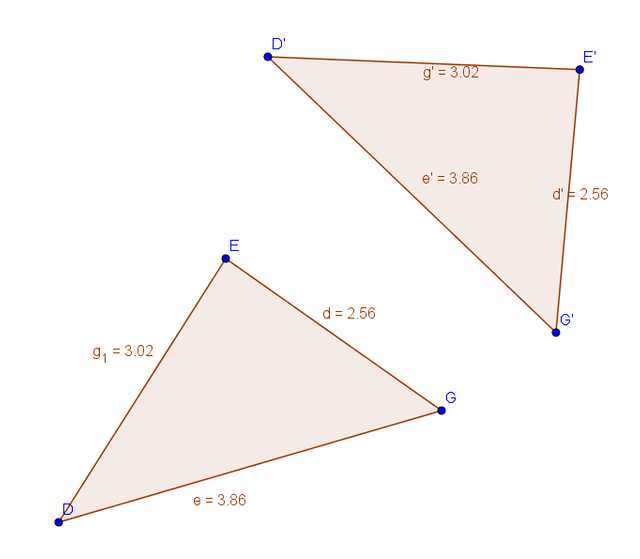
It doesn't matter the orientation of that carbon copy, if we were to overlap the two triangles, all three pairs of corresponding sides and angles would be equal.
I would always demonstrate this by giving two students on different sides of my room three unsharpened pencils of the same length to tape together to form a triangle. I would have them come up to the front board and compare for the class. Obviously, both triangles would be the same. Even if one was rotated, you could rotate the other to line up exactly with the other.
So, all our other working postulates, AAS, SAS, ASA, HL, etc. would follow the same logic.
So, what about one that doesn't work?
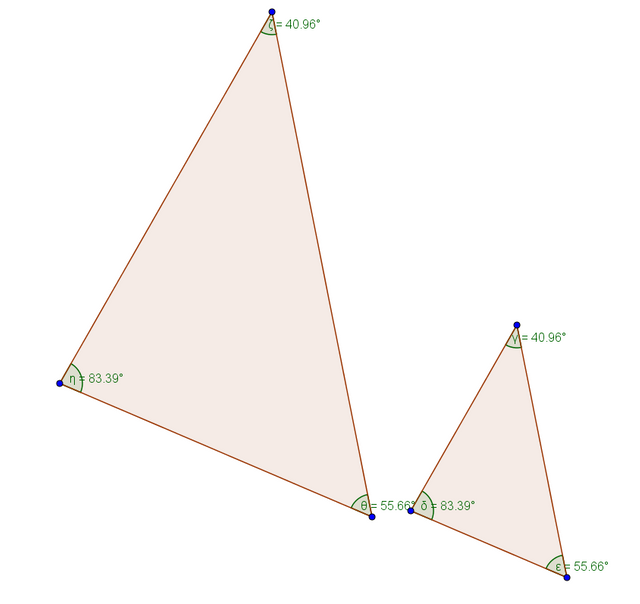
Let's consider AAA, or "Angle Angle Angle". What is the logic here?
If I know information about just three angles of a triangle, it it sufficient enough information to construct an exact carbon copy of it?
As it turns out, sometimes you get lucky and will be able to. But, most of the time, you would get a triangle that is similar to your original triangle and not congruent.
Now, some ASS
Or, Angle Side Side, to be exact. What is so wrong about it?
Case 1: No Such Triangle Exists
Let's consider being given information about an specific Angle, Side, and Side. Say for a Triangle ABC, a = 6, A = 45° , and b = 12. What would happen?
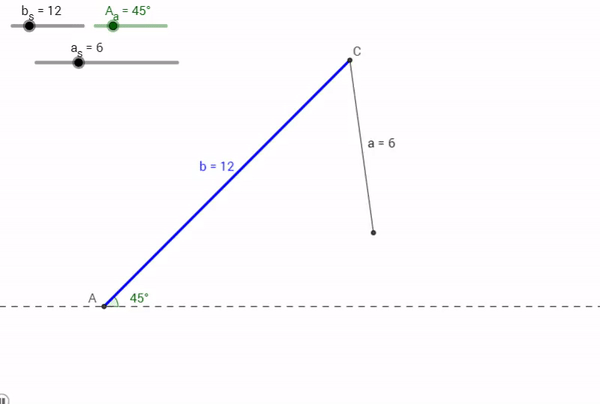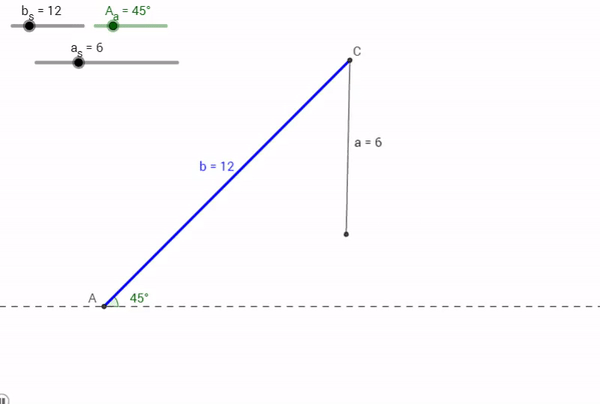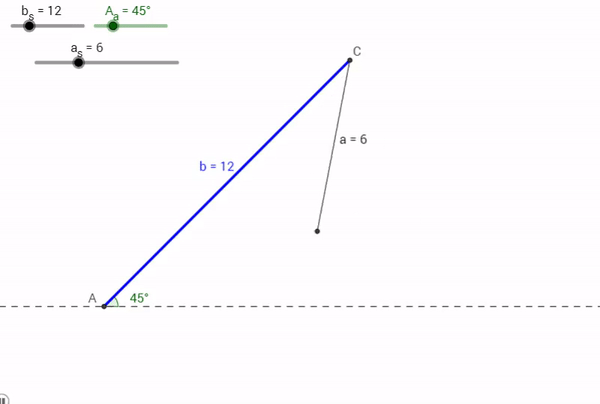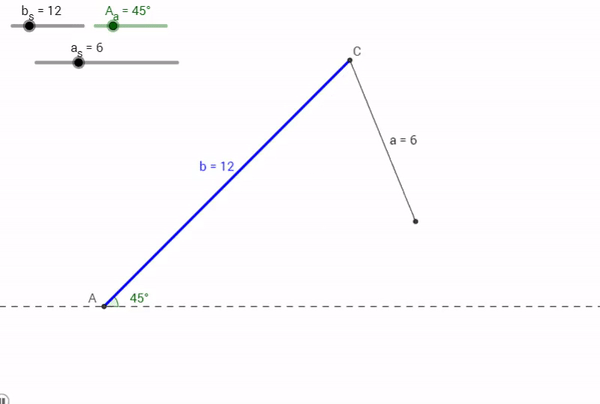
Just like the sad T-rex that can't clap his hands, no triangle could possibly be made from this combination
You learn later on in Precalculus exactly why. Namely, the Law of Sines that states for any triangle ABC the following ratios should always be in proportion:
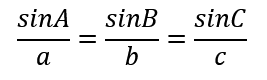
For the combination above, it is impossible to solve for the missing angle B:
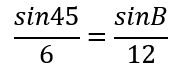
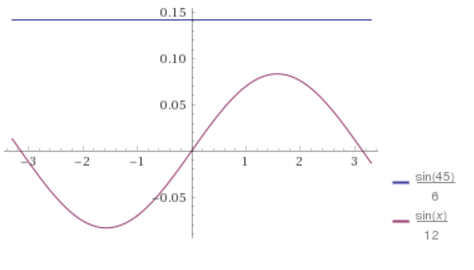
Case 2: Two Such Triangles Exist
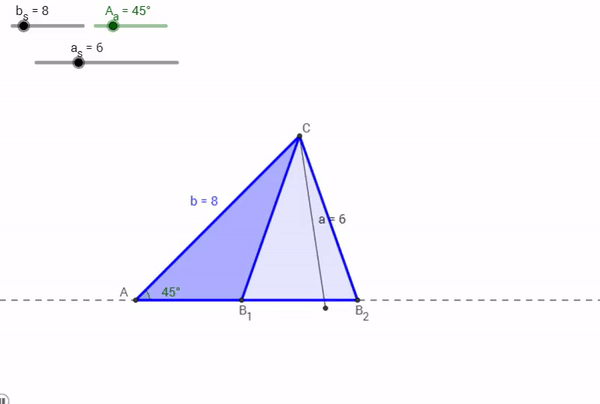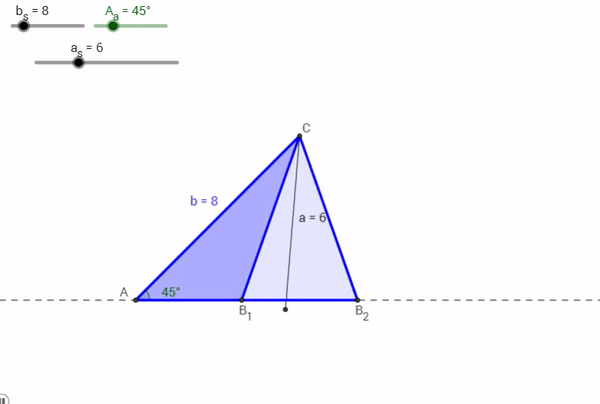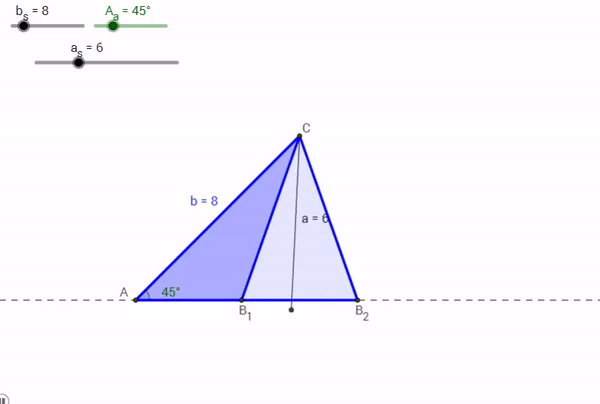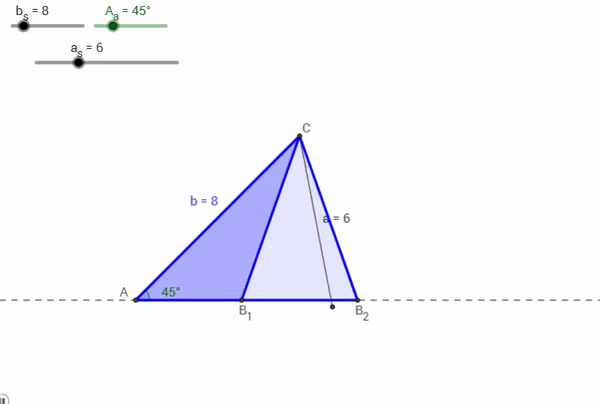
Now, say for a Triangle ABC, a = 6, A = 45° , and b = 8. What would happen?
As it turns out, two triangles could be made with that particular information. One, an obtuse triangle (in dark blue by the points A, B1, and C above), another an acute triangle (in light blue by the points A, B2, and C above). The mechanism driving this, again, is the Law of Sines.
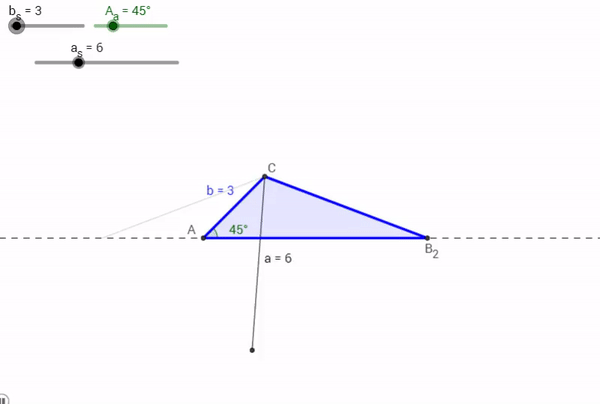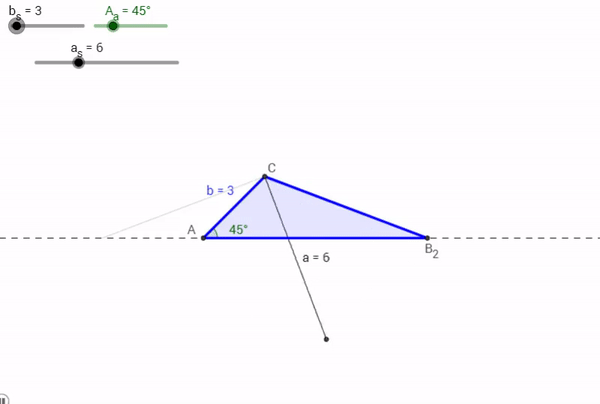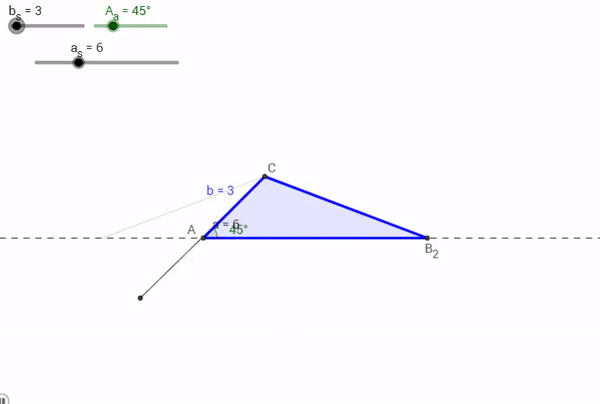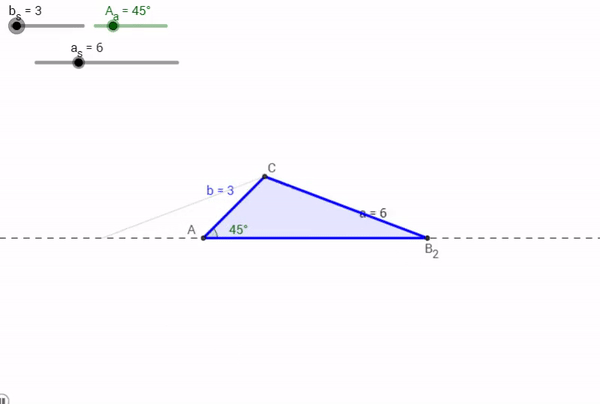
Case 3: One Such Triangle Exists
This is the case where we would get lucky and produce an exact copy of an original triangle with a given Angle Side and Side. But again, this is just us getting lucky being constrained by the original information given to us.
In the end, ASS is ambiguous!
We just cannot guarantee that we will produce a carbon copy of our original triangle, therefore rendering ASS useless as a postulate for triangle congruency.
However, we render it hilarious for geometry students both old and young to say out loud and chuckle to themselves. Showing us that time and time again, math gives us these funny little moments. At least if we understand where to find them.
Want to play with the applet that shows the ambiguous cases of Angle Side Side made in this article??
Visit this link for the Geogebra demonstration.
Steemit Board Awards - Click Below for More Information





cute
Aww, thanks!
lol I remember sitting in geometry class and my professor making a stupid joke about this! Great post! Did you make the Geogebra demonstration? (Also how do you make the pictures of LaTeX math in your pages?...do you just take screenshots from a compiled LaTeX doc?)
wait until you name an octagon BUTTHOLE
wow! Good info! Just followed! Follow me, too? :)
Hello! I just upvoted you! I help new Steemit members! Upvote this comment and follow me! i will upvote your future posts! To any other visitor, upvote this post also to receive free UpVotes from me! Happy SteemIt!
High quality, as always - many thanks!