Elements of Set Theory: Baby set Theory
We'll start our discussion, again, with some basic concepts of set theory. Much of the material here will be familiar to you if you've read some of my readings on the gentle introduction to the art of mathematics. But it is a common practice in each mathematics to start with set theory discussion. But here, we will just review some elementary set theory (and do it in our notation). In this particular section, we'll not get involve with rigor for the mean time - serious works starts at chapter 2.
Baby set Theory
Informally, a set is just a collection of things (called its members or elements), the collection being regarded as a single object. We write " " to say that t is a member of A, and we write "
" to say that t is a member of A, and we write "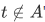 " to say that t is not a member of A.
" to say that t is not a member of A.
Consider the following set  whose members are exactly the prime number less than 10,
whose members are exactly the prime number less than 10,
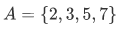
Another example of set is the following: let 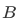 be the set of all solutions to the polynomial equation
be the set of all solutions to the polynomial equation
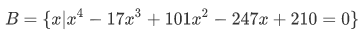
If you are an industrious reader you can verify that,
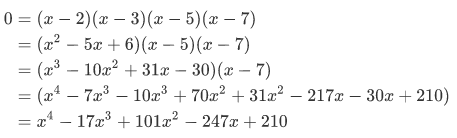
So it turns out that the set 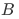 has exactly the same four members
has exactly the same four members 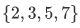 as
as 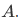 . Hence we can say that they are the same, i.e.,
. Hence we can say that they are the same, i.e., 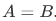 . It does not matter how we define
. It does not matter how we define  and
and  , as long as they have the same elements, they are equal. From this we can formulate a general principle.
, as long as they have the same elements, they are equal. From this we can formulate a general principle.
Principle of Extensionality
If two sets have exactly the same members then they are equal.
Now, let's express this utilizing some basic notations. Also we abbreviate the phrase "if and only if" using "iff". The restatement would be:
We write to mean that A and B are the same object.
to mean that A and B are the same object.
On the other hand, we write 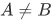 to mean the converse of
to mean the converse of  .
.
Null Set/Empty Set
A small set would be a set 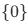 having only a single member, the number 0. But there is actually a smaller set than that, known as the null set or the empty set. This kind of set has no member at all. One might ask how useless or even frivolous this set would be.
having only a single member, the number 0. But there is actually a smaller set than that, known as the null set or the empty set. This kind of set has no member at all. One might ask how useless or even frivolous this set would be.
In the future we'll utilize the power of null set or empty set, from this set using various set-theoretic operations surprising array of sets can be constructed.
Note the following set having a member of x and y only: 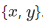 . It follows that
. It follows that 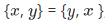 , since both sets have exactly the same members. A special case x = y would give us
, since both sets have exactly the same members. A special case x = y would give us 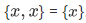 .
.
We can form a set whose member is only the empty set 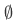 which is given as
which is given as 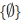 .
.
Note that, 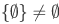 , because
, because 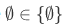 which implies that
which implies that 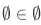 but this is not the case because
but this is not the case because 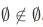 .
.
This fact is better reflected as,
a man with an empty container is better off than a man with nothing - at least he has the container.
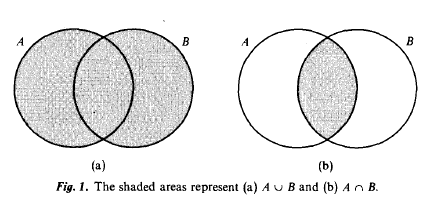
Union and Intersection
The usual Venn diagram depicting these operations:
Subset and Inclusion
A set A is said to be a subset of a set B iff all (including the subset of A if it has) members of A are also a member of the set B.
- the empty set
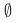 is a subset of all set
is a subset of all set - we say that A is included in B or that B includes A if A is a subset of $B$ or
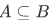
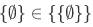 but
but 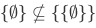 , since
, since 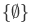 has a member, namely
has a member, namely 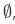 that is not a member of
that is not a member of 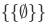 .
.- Given a set
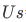 = "set of all people in the US",
= "set of all people in the US", 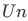 = "set of all countries belonging to the United Nations", then
= "set of all countries belonging to the United Nations", then 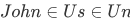 , but note that
, but note that 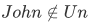 (he is not a country), and hence
(he is not a country), and hence 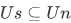 .
.
Power Set
Any set A can have one or more subsets and we can gather these subsets into a collection - forming what is known as the power set P. For instance, the power set of A is given as P(A).
Consider the following example,
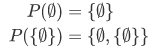
Method of Abstraction
Method of abstraction is a very flexible way of naming a set, as we include in the expression the restrictions and conditions (entrance requirement) that the element has to follow. The notation used for the set of all objects x such that the condition 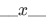 holds is,
holds is,
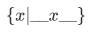
Examples:
Dangers Inherent in Abstraction
Consider the following set, 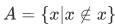 - "a set of all objects that are not element of themselves". If
- "a set of all objects that are not element of themselves". If 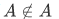 then it meets that condition of the abstraction entrance requirement for, whereupon
then it meets that condition of the abstraction entrance requirement for, whereupon 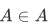 . On the other hand, if
. On the other hand, if 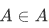 then A fails to meet the entrance requirements thus
then A fails to meet the entrance requirements thus 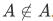 . This problem that both
. This problem that both 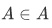 and
and 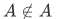 are attainable is called the Russell's paradox.
are attainable is called the Russell's paradox.
This paradox is avoided by introducing two distinct mathematical objects - sets and classes.
- any collection of sets will be a class
- some collection of sets will be a set
- some oversize collections will be called a proper classes
Disclaimer: this is a summary of section 1.1 from the book "Elements of Set Theory" by Herbert B. Enderton, the content apart from rephrasing is identical, most of the equations are from the book and the same examples are treated. All of the equation images were screenshot from generated latex form.



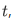
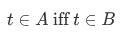

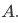
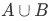
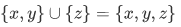

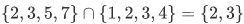
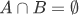
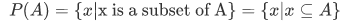

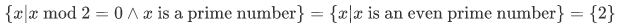
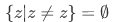
You got a 8.59% upvote from @redwhale thanks to @sinbad989!
Earn 85% earning payout by delegating SP to @redwhale
If you are looking to earn a passive no hassle return on your Steem Power, delegate your SP to @redwhale by clicking on one of the ready to delegate links:
25SP | 50SP | 75SP | 100SP | 250SP | 500SP | 1000SP | 2500SP | 5000SP Another Amount
You will earn 85% of the voting bot's earnings based on your delegated SP's prorated share of the bot's SP each day! You can also undelegate at anytime.
Our Discord Channel: https://discord.gg/ttaypWb
You got a 4.76% upvote from @nado.bot courtesy of @sinbad989!
Send at least 0.1 SBD to participate in bid and get upvote of 0%-100% with full voting power.