In this book, Elements of Set Theory, the axioms of set theory well be stated (in the future sections), and we are going to show that our theorems are consequences of those axioms.

The great advantage of the axiomatic method is that it makes totally explicit just what our initial assumption are.

It is sometimes said that, "mathematics can be embedded in set theory." This means that mathematical objects (such as numbers and differentiable functions) can be defined to be certain sets. And the theorems of mathematics (such as the fundamental theorem of calculus) can be viewed as statements about sets.

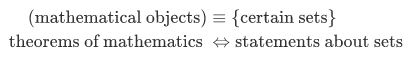
Hence our axioms provide a sufficient collection of assumptions for the development of the whole of mathematics - a remarkable fact.

Nonaxiomatic approach to set theory is often referred to as "naïve set theory". Historically, set theory originated in nonaxiomatic form. But certain assumptions in naive set theory were inconsistent and was totally untenable (e.g. Russell's paradox). This forced the development of axiomatic set theory.

Our selection of axioms will be guided by the desire to reflect as accurately as possible our informal ideas regarding sets and classes.

Axiomatic Method

---

Our axiom systems begins with two primitive notions, the concepts of "sets" and "members". In terms of these concepts we will define others.

But note, the primitive notions remain undefined. What we will do is adopt a list of axioms concerning the primitive notions. This axioms somehow divulge partial information regarding the meaning of the primitive notions.

Now that we have a list of axioms, we will then proceed to derive sentences that are logical consequences (theorem) of the axioms. A sentence 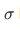is said to be a logical consequence of the axioms if any assignment of meaning to the undefined notions of set and member making the axiom true also makes 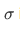true.

An interesting take on the foundation of mathematics concerns the existence of a finitely long proof of from the axioms. Based on the results of mathematical logic, the answer to this existence question is affirmative - there exists a finite "proof".

^{Disclaimer: this is a summary of section 1.4 from the book "Elements of Set Theory" by Herbert B. Enderton, the content apart from rephrasing is identical, most of the equations are from the book and the same examples are treated. All of the equation images were screenshot from generated latex form using typora.}

1. Elements of Set Theory by Herbert B. Enderton

Thank you for reading ...