A Powerful Generalization of Mathematics

source: pixabay
As a physics student, it is natural for me to describe and analyze complex phenomena in terms of its fundamental elements. This approach to thinking, done by reducing a complex system into its fundamental parts, is called reductionism.
Reductionism
The idea of reductionism was first introduced by Descartes in his work “Discourse” in 1637[1]. Descartes argues that nature was a just a giant clock, not a living organism, but a machine. [2]
[the machine] could be understood by taking its pieces apart, studying them, and then putting them back together to see the larger picture[2]
I started adopting this philosophy in my quest to learn almost all the knowledge that is available. I believe that by reducing a domain of knowledge into its fundamental parts, it was easier to learn its details. I realize this when I started learning object-oriented programming where I started to adopt a thinking that “everything is an object”. I was introduced to the idea of reducing a system into its fundamental parts or properties and functions.
For instance, consider the genus of canine, they share the same kind of properties, they have tails, they have four legs - they almost have the same generic form. They also share common function or action, e.g. they bark. From these fundamental properties, you can instantiate a bulldog by setting up its skin, its height, etc. And add some action or function features, e.g. bark or roll.

source: wiki
When you think about it, there must be a way to reduce mathematics into its fundamental parts. From the previous post, the notion of sets, we’ve encountered Category theory on how mathematicians found a relationship between different areas of mathematics. This is a hint of an underlying unifying concepts of mathematics.
Mathematics
Just like pornography, when we see mathematics we know it when we see it. But what is mathematics? A common answer is mathematics is about proof. They have a standard workflow that follows:
- a sequence of definitions
- introduction of several lemmas
- a statement of a theorem
a. a proof that applies the lemmas to the definition
This is the universal mathematics workflow: “definition-theorem-proof”. After doing all those steps in the workflow what you have now is a new knowledge true to the span of the lemmas and definitions.
Today, we have several axioms available, and working on one set determines what “mathematical system” is being worked on. That’s why we have Euclidean and non-Euclidean geometry, Riemannian and semi-Riemannian manifold, Cantorian and non-Cantorian set theory, etc.
This brings us to the Bourbaki.
Root of Mathematics
A set of French mathematics students revolted against the “semi-intuitive” view championed by Poincare and started a “new” formalism of mathematics in 1939. It was known as the Bourbaki movement, under the pen name “Nicholas Bourbaki”. [3]
The Bourbaki realized that there are “roots” of mathematics –something that was true of mathematics in general. They have identified three basic “mother structures” upon which all of the mathematics depends. These basic structures are called:
This list has been extended as of now, with additions of measures, metric structures, events, equivalence relations, differential structures, and categories.
Note that a structure is just an additional object on a set [4]. These mother structures all require a set. They also required something called a relation.
Fundamental Parts
Our basic notions of the set are just a collection of things, referred to as the “element of a set”, which defines the constituent of a mathematical object. A relation/function, on the other hand, is a transformation that acts on a set to produce another set.
This is not enough, a set plus a relation/function does not provide us enough to say we have a structure. An additional thing we need are rules of how this set and relation/function interact.
For a mathematical structure to exist, we need a set, a relation/function, and their rules of interaction.
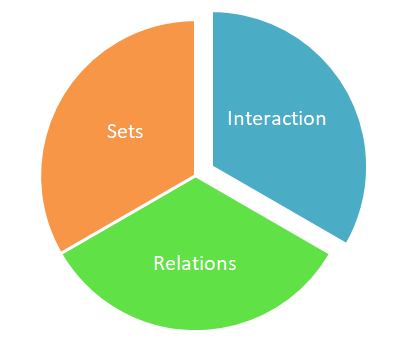
Mathematics Fundamental Parts
Learning mathematics is like building a house. You lay the foundation brick by brick. The mathematical structures serves as our brick in building mathematics.
References
[1]. https://www.philosophybasics.com/branch_reductionism.html
[2]. http://www.eoht.info/page/Cartesian+reductionism
[3]. https://en.wikipedia.org/wiki/Nicolas_Bourbaki
[4]. https://en.wikipedia.org/wiki/Mathematical_structure


Las matemáticas son una de las primeras ramas que vemos en esta vida, es bueno que nos cuentes sobre ello, ya que es algo que una vez saliendo de las escuelas olvidamos.
Thank you for trying to explain the architecture of mathematics. But I don't think, it's a good idea to take reductionism as base of an otherwise good essay. Reductionism has long been outdated and replaced by systems theory. Rather than breaking down the math, you could first build it from the individual disciplines and then show synergies between the disciplines, right up to the Langlands program, which seeks to reconcile the different disciplines.
This is a good suggestion. I've read a few article about this Langlands programs, and just like the theory of everything for physics, there's just too many things to get good at before one can get a grasp of the subject.
By systems theory, you mean the "emergentism"? I've sit-in a class once in complex systems, and I was convinced by that time that, maybe, all the physical laws we have about have some collective origin. There is a need, now more than ever, a full understanding and ways of modeling systems that spit emergent behavior naturally.
Are we in the same line of thinking?
This post has received gratitude of 1.95% from @appreciator courtesy of @sinbad989!
You have been upvoted by @nextvote. Interesting philo-mathematics concept! thank you.
Congratulations @sinbad989, this post is the fifth most rewarded post (based on pending payouts) in the last 12 hours written by a Newbie account holder (accounts that hold between 0.01 and 0.1 Mega Vests). The total number of posts by newbie account holders during this period was 4506 and the total pending payments to posts in this category was $4349.63. To see the full list of highest paid posts across all accounts categories, click here.
If you do not wish to receive these messages in future, please reply stop to this comment.
That was quite interesting and informative @sinbad989! Thankss for sharing :)
Just to add a bit of transparency as to why the reward on this post is so high
Ah, math! It was a bane in elementary but in highschool out teacher made it fun and I actually came to love it. After studying probability and statistics I was amazed what you can learn , discover and do with math. Kudos and hats off to all mathematicians.