A Gentle Introduction To Mathematics - Parity and Counting Arguments
Parity and Counting Arguments
Two very powerful elements of the proof-making arsenal:
- Parity – a way of referring to the result of an even/odd calculation
- Counting arguments – most often in the form of counting the collection in two different ways
These two techniques when applicable tend to produce really elegant little arguments.
ASCII (American Standard Code for Information Interchange)
Paper cards were used to store information in the very early days of computers. The so-called “punch card” was used to store binary information by means of holes punched into it.

IBM 650 computer at Texas A&M University where punchcards where Gods
Tapes and cards could be “read” either by small sets of electrical contacts which would touch through a punched hole to be kept separate if the position wasn’t punched, or by using a photo-detector to sense whether light could pass through the hole or not.
These paper media were amazingly useful but would require a couple of large cabinets to store what can now fits in a jump drive which one can wear on a necklace.
Binary information was ideal for paper media. But of course, people needed real data in alphanumeric (both alphabetic characters and numeric characters). Several encoding schemes were introduced, translating between the character sets that people commonly used to the binary numerals that could be stored on paper.
One of these schemes still used today is the ASCII (American Standard Code for Information Interchange). It uses 7-bit binary numerical to represent characters. And so 2^7 gives us 128 different symbols. This is more than enough to represent upper and lower case letters, the 10 numerals, and the punctuation marks. The remaining spots in the ASCII code were used to contain the so-called “control characters”.
These control characters are why modern keyboards still have a modifier key labeled “Ctrl” on them. The following listing gives the decimal and binary numerals from 0 to 127 and the ASCII characters associated with them – the non-printing and control characters have 2 or 3 letter mnemonic designation.
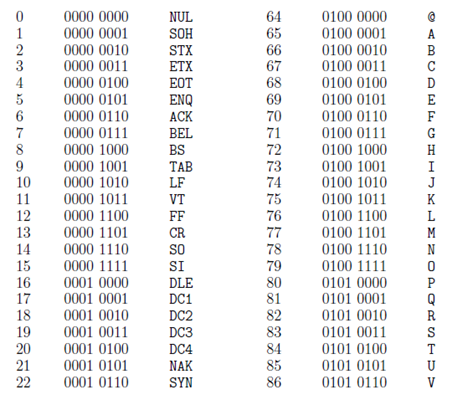

128 different ASCII characters
You may have wondered why there are 8 bits for each representation, note however that the left-most bits in all of the binary representations above are 0. Now it takes only 7 bits to encode the 128 values in the ASCII system.
Most computers use 8-bit words or “bytes” as their basic units of information, and the fact that the ASCII codes only requires 7 bits lead someone to think up a use for that additional bit. It became a “parity check bit”.
If the seven bits of an ASCII encoding have an odd number of 1’s, the parity check bit is set to 1 – otherwise, it is set to 0. This results to all of the 8 bit words to have an even number of 1’s.
This is an example of a so-called error detecting code known as the even code or the parity check code.
Due to noise in telecommunication channels there are chances that “bit error” will be introduced in a transmitted encoding. (There are other more advanced coding schemes.)
Graphs
The application of graph was first used by Leonhard Euler to solve a problem posed by the citizens of Konigsberg, Prussia.
Konigsberg was situated at a place where two branches of the Pregel river come together – there is also a large island situated near this confluence.
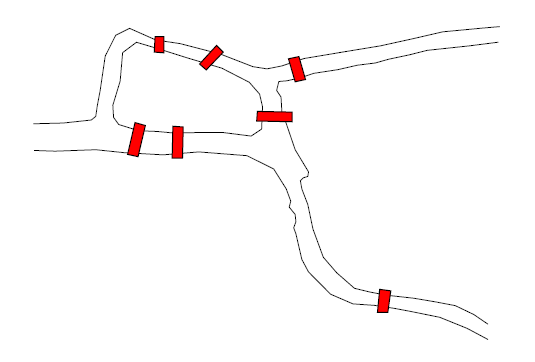
simplified map of Konigsberg, Prussia
A network of seven bridges had been constructed to connect all these land masses. The townsfolk want to know whether it was possible to leave one’s home and take a walk through town which crossed each of the bridges exactly once and, finally, return to one’s home.
Euler was able to answer this question by converting the map of Konigsberg into a graph and then making some observations on the parities of the nodes in this graph. It was found that it can’t be done; crossing each of the bridges exactly once and, finally, return to one’s home.
The “parity of a node” is shorthand for the “parity of the degree of the node”.
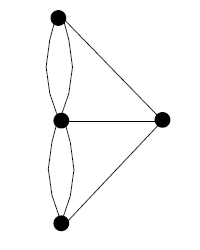
the undirected graph representation of the Konigsberg seven bridges
The undirected graph has 4 nodes: one of 5 degrees and 3 of degree 3. (degree is the number of connections)
In a simpler statement: all graphs have an even number of odd nodes.
The question of whether a graph having a given list of vertex degrees can exist comes down to an elegant little argument using both of the techniques in this section. We count the edge set of the graph in two ways – once in the usual fashion and once by summing the vertex degrees, and since the latter count is actually a double count we can bring in the concept of parity.
Pruned Board
Another lovely argument involving parity arises in questions concerning whether or not it is possible to tile a pruned chessboard with dominoes.

a 5x5 checkerboard for you to help imagine
Suppose we have dominoes that are fit if they are laid on a chessboard that they perfectly cover two adjacent squares. The question is quite simple:
Is it possible to perfectly tile an mxn chessboard with such dominoes?
What does it mean when you say “perfectly”?
By “perfectly tiling” a chessboard we mean that every domino lies on the board, covering precisely two squares, and that every square of the board is covered by a domino.
Answer: if one of the m or n is even it can be done. If both m and n are odd we will be out of luck.
Going back to our original question of whether it was possible to cover a pruned board, we then need to define what it means to be pruned.
A “pruned board” is obtained by either literally removing some of the squares or perhaps by marking them as being off limits in some way.
Two tiling problems regarding square chessboards
- An even-sided square board (e.g 8x8 board) with diagonally opposite corners pruned
- An odd-sided board with one square pruned.
The pattern of black and white is sort of an artificial parity, in a way that if we number the squares, the black would be even square while the white will be odd squares.
An odd-by-odd chessboard has more squares of one color than of the other. Thus it has to be pruned for it to be tiled by dominoes but it has to be the right color.
Each domino covers two squares - on of each color! So the pruned board must have the same number of white squares as black.
Magic square
A magic square is a square nxn array containing the numbers The definition of a magic square requires that the numbers be arranged in such a way that every row and column sum to the same number (the magic sum).
Consider the following magic square of n=3:
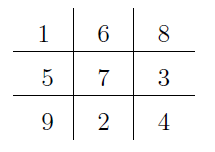
Can we produce another magic square of n=3 having different magic sums?
This is conceivable; there is actually a theorem that states that the magic sum is determined completely by n.
Proof:
The sum of all entries in the magic number is
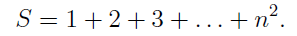
From the formula for the sum of the first k naturals:
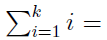
If we replace k= , the sum of the first k naturals becomes:
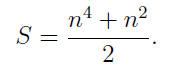
We then let the magic number be M, then since it’s a square, the sum of all entries S has to be a multiple of M, that is,
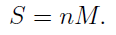
Disclaimer: this is a summary of section 7.2 from the book A Gentle Introduction to the Art of Mathematics: by Joe Fields, the content apart from rephrasing is identical, most of the equations are screenshots of the book and the same examples are treated.


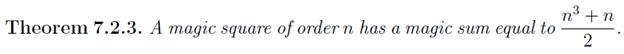
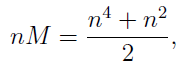
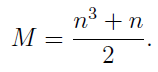
You got a 10.49% upvote from @brupvoter courtesy of @sinbad989!