A Gentle Introduction To Mathematics - Other proofs using PMI
In the previous post, long time ago, we talked about an application of the principle of mathematical induction in proving statements, for instance, sums and product rules. In this section, we will explore the divisibility side of statements including some inequalities. It is shown that PMI can be a great asset in proving statements after all. (though sometimes it requires some tricks)
Divisibility Statements
Fermat’s Last Theorem (FLT):
For every prime number p, and for all integers x, the p-th power of x and x itself are congruent mod p.
Symbolically,
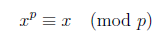
A restatement of FLT is that p is always a divisor of x^p – x (assuming p is a prime and x is an integer). Fermat’s little theorem allows math professors to cook up divisibility results that can be proved by using mathematical induction.
Consider the following:
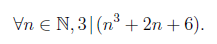
Note that we can recast the equation above into,
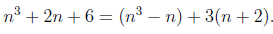
Let’s have a look at proving this statement using PMI:
Clearly, for n=0,  | 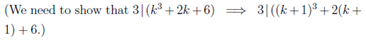 |
| -- | 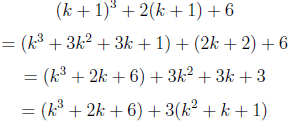 For the first term to be divisble by 3, there must be an integer m such that 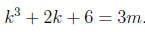 |
| -- | 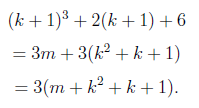 Q.E.D. |
Another Example:
Consider the following theorem:
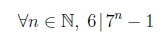
Notice that 7 is equivalent to 1 (mod 6) (this means that if you divide 7 by 6 remainder is 1), the theorem says that if we raise 7 to an arbitrary power of n and subtract 1, the result is divisible by 6.
A proof of a statement like this requires another little trick.
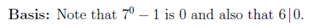 |  |
| -- | 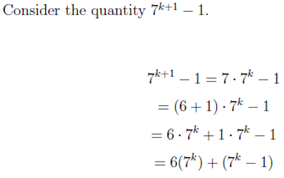 |
| -- | By the inductive hypothesis, 7^k – 1 is divisible by 6, so there must be an integer m such that 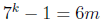 It follows, 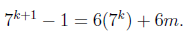 Q.E.D |
Inequality Statements
We have given two examples of divisibility proof using PMI. Mathematical induction can also be used to prove inequalities.
Consider the sequences,
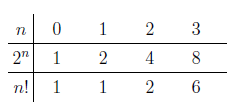
For small values of n, 2^n > n! But from n =4 onward the inequality is reversed.
The statement of the inequality that we want to prove goes like this:
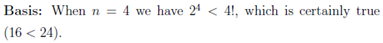 | For k > 4, and for the induction, we assume n = k + 1 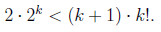 so, 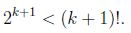 Q.E.D |
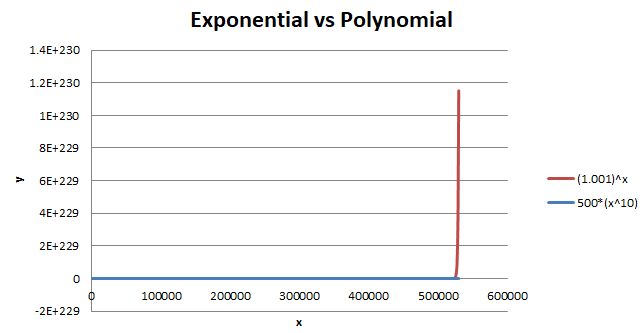
Interestingly, in calculus, it is well known that exponential functions grow faster than polynomial functions.
For completion, consider the exponential function (1.001)^x, and the polynomial p(x) = 500x^10. This may be hard to believe but even, b^x is eventually larger than any polynomial p(x).
Disclaimer: this is a summary of section 5.3 from the book A Gentle Introduction to the Art of Mathematics: by Joe Fields, the content apart from rephrasing is identical, most of the equations are screenshots of the book and the same examples are treated.


This post has received a 1.04 % upvote from @drotto thanks to: @sinbad989.
excellent publication and I voted, I invite you to observe my post about mathematical science, greetings.
You got a 3.85% upvote from @allaz courtesy of @sinbad989!