A Gentle Introduction To Mathematics - Ordering relations

sinbad989 (52)in #mathematics • 6 years ago (edited)

Ordering Relations

The prototypical symbol for ordering relations is , another example of ordering relation is . Note, however, that they are different in two aspects: first is that one doesn’t contain similar elements, second is that one is reflexive while the other is irreflexive.

Total Ordering

The relation imposes what is known as total order on the sets that it acts on. In total ordering, also known as linear ordering, every pair of elements can be compared and we can use the ordering relation to decide which order they go in.

Partial Ordering

There is also what is called a partial ordering, in which some elements of the set are incomparable. Complex numbers is a good example of partial ordering, they are incomparable when the complex part exist.

Partial Ordering Set (poset)

A set together with an ordering relation creates a mathematical structure known as a partially ordered set (abbreviated as “poset”). To identify a “poset”, one has to specify a set S and an ordering relation R. To denote a poset we write, .

Hasse Diagram

Hasse diagram is used to display “poset” in a more succinct way than a digraph. There are features of a Hasse diagram that corresponds to the properties of an ordering relation. For the reflexive properties, we leave it out in Hasse diagrams. In anti-symmetric property, vertices are arranged so that its direction is always upward, leaving out the arrowhead. For the transitivity property, we leave out the connections as well.

Consider the following digraphs and Hasse diagram

digraph	Hasse diagram

Graded Posets

There are element features that allow us to consider the ordering in Hasse diagram in terms of a “rank”.

Consider the set of all subset of 3 elements (power set) , this set can be partially ordered using the relation. By partially ordered we mean that some elements of this set not reflexive, anti-symmetric or transitive. The power set ordered relation in Hasse diagram is drawn as,

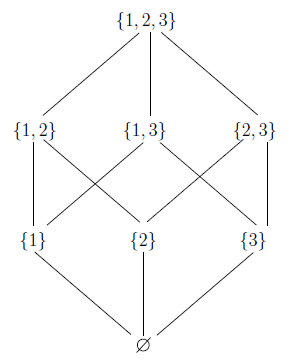
The posets can be laid out in ranks are known as graded posets, which means that those of the same rank are always incomparable. For the power set, the rank of and are equal hence, they are incomparable. These are the reason why we consider it only partially ordered.

Example

Another interesting example of a graded poset is the set of divisors of some number partially ordered by the divisibility relation . In this case ranks (grading function) are based on the sum of all the exponents appearing in its prime factorization.

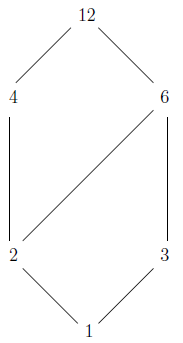
Hasse diagram of a poset 72

Other terminology related to POSET

Chain: a subset of the elements of POSET all of which are comparable
- Example:
- A chain is a total ordered set
Anti-chain: a subset of the elements, none of which are comparable
- Example:
- A subset of the same rank are anti-chain in a graded POSET
Maximal: refers to the chain or anti-chain that cannot be extended by adding another element
- Example:
- A chain which is maximal must contain a maximal and minimal element
- Collections of all maximal elements or minimal elements forms an anti-chain
Greatest element/Top: the apex of the Hasse diagram, an element that is greater than every other element
- Example:
Least element/Bottom: the element that is smaller than every other element
- Example:

_{Disclaimer: this is a summary of section 6.3 from the book A Gentle Introduction to the Art of Mathematics: by Joe Fields, the content apart from rephrasing is identical, most of the equations are screenshots of the book and the same examples are treated.}