A Gentle Introduction To Mathematics - Functions
The most useful abstractions in mathematics is the concept of function, which can be further abstracted.
Another mathematical object that acts like functions is an operator, an entity that devours functions as functions find numbers more edible. The most famous operator is the “differentiation”, capable of transforming (derivative) a function into another function.
When it comes to using a function, two different people using the same function and similar input most give a matching answer. If they’re different, then at least one of them must wrong. This is a way to ensure that a function is “well-defined”.
Functions
A more formal definition is given as follows:
One can think of a function as a special type of binary relation, we have the form 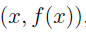 , with an input and a corresponding output. Note that we’ve encountered a similar binary relation as a Cartesian product associated with
, with an input and a corresponding output. Note that we’ve encountered a similar binary relation as a Cartesian product associated with 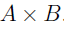 .
.
Note, that not all values can serve as an input of a function (e.g. square root of a negative), similarly some outputs are not possible. Thus in dealing with a function as a relation contained in 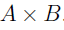 , there are actually four sets that are of interest – the sets A and B and some sets which we will denote by A’ and B’.
, there are actually four sets that are of interest – the sets A and B and some sets which we will denote by A’ and B’.
For a better understanding of the four sets, consider the following visualization:
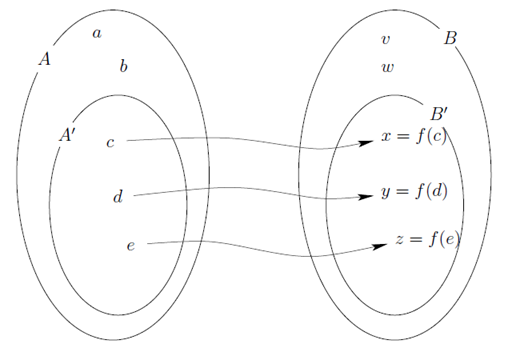
functional relation of domain, codomain and range
Only 3 of the sets were baptized. The set A’ is called the domain of the function f. The set B’ is known as the range of the function f. The set B is called the codomain of the function f. The input set A does not have a name. It was natural to rigged the definition of a function to merge A and A’ into one set. Hence, there is only one set on the input side – the domain of our function.
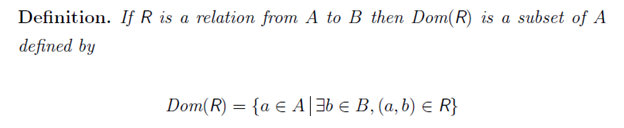
We write the domain of a relation R 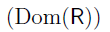 . We write
. We write 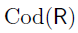 to refer to the codomain of the relation,
to refer to the codomain of the relation, 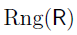 to refer to the range.
to refer to the range.
We now have an idea that functions are just special classes of relations; it is natural to say that function is just a set of ordered pairs. Basically, the function is tied up to the rules that give the output and the type of input given.
For instance, the function 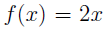 defined on
defined on 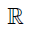 is a different animal from the function
is a different animal from the function 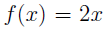 defined on
defined on 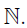
In specifying a function precisely, one must define its domain as well as a formula for it. Conventionally, this is given by writing a formula then a semicolon then a domain.
Now, we are ready for the real definition of a function.
Formal Definition of Function
A function must have its domain equal to the set A (where inputs come from). We say that the function is defined on its domain.
Surjection
A function’s range and codomain may be different. In the event that they are equal, we say that the function is surjective.
Given an element x and y, of the domain and codomain, and 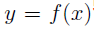 , then one say that
, then one say that
- y is the image of x
- x is a preimage of y
Note the different articles, a and the, used in the phrases. These emphasize that y is uniquely determined by x but not vice versa.
- 4 is the image of 2
- 2 or -2 could either be a preimage of 4
In summary, if a function is surjective, every element of the codomain has a preimage.
Preimage Notation
One commonly used notation to refer to the preimage of some element, y, of the range is 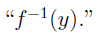 . By writing
. By writing 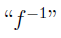 you are making a rather vast presumption that there is exist a function that serves as an inverse for f.
you are making a rather vast presumption that there is exist a function that serves as an inverse for f.
One can define an inverse for any relation; the inverse is formed by simply exchanging the elements in the ordered pairs that make up R.
In the graphical representation, the inverse is just a reflection of the original relation in the line y = x. Note, however, that it is possible that one, both or neither of these to be functions.
Example
Consider the graph of 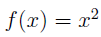 and its inverse.
and its inverse.
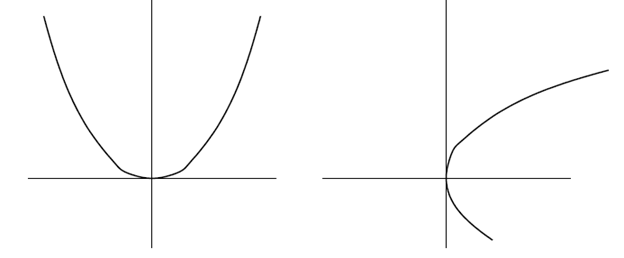
Left: original function, right: inverse function
The inverse function doesn’t pass the vertical line test (uniqueness of the range value), thus its not really a function but merely a relation. The function 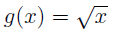 is not truly a function.
is not truly a function.
The interesting part of this inverse function is that it makes a specific choice. If we start with a negative number (e.g. -3) and square it, we get a positive (e.g. 9), and if we try to get its inverse (square root), we get another positive number (e.g. 3). This is clearly unacceptable because we did not end up with what we ought to get as per function definition.
Let’s consider the case now, where the inverse of a function is a function.
Inverse function
Under what circumstances does the inverse pass the vertical line test?
When the original function passes the so-called horizontal line test (every horizontal line intersects the graph at most once)
An example of a function that passes the horizontal line test is the cube of an input: 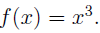 This function is said to be injections, same as saying that it is “one-to-one.”
This function is said to be injections, same as saying that it is “one-to-one.”
Injective functions
Injective functions can be inverted – the domain of the inverse function of f will only be the range, Rng(f), which as we have seen may fall short of the being the entire codomain, since 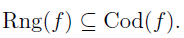
The best way of thinking injective functions is in terms of preimages – when a function is injective, preimages are unique.
There are instances that a function is both injective and surjective (one-to-one and onto). These functions are known as bijective.
Bijective
Bijective is important as it allows mathematician to match every elements of two sets. You will probably spend a good bit of time in the future devising maps between sets and then proving that they are bijections.
The way to show that a function is bijective is to prove that it is both a (1) surjection and an (2) injection.
1. Surjective proof: finding the existence of an element for an image
Inverse function is important in this part, so if one finds the inverse function easily then it is easy to find a preimage for an arbitrary element. Here we are talking about a constructive proof of an existential statement.
Given the definition of surjective:
A function f is surjective iff for all y which is an element of the codomain there exist an x which is an element of the domain such that y = f(x).
In mathematical notation, we want to prove this:
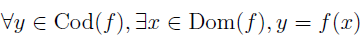
Find the x that works for an arbitrary y.
2. Injection proof: finding the uniquess of an element for an image
In injection, we consider two distinct elements of  :
:  and
and  and that
and that 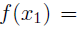
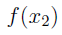 . We want to show that
. We want to show that 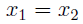 .
.
“Images” and “Preimages” of Sets
The ideas of “images” and “preimages” can be extended to sets.
If S is a subset of dom(f) then the image of S under f is denoted f(S) and
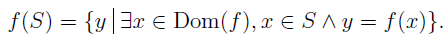
If T is a subset of Rng(f) then the preimage of the set T under f is denoted
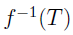 and
and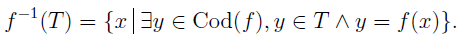
Restating Surjective and Injective
With the extended f to cover the power set of its domain and range. We can now introduce a new meaning of surjective and injective functions.
- A function f is surjective iff
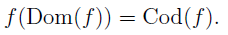
- A function f is injective ff the inverse images of singletons are always singletons. That is,
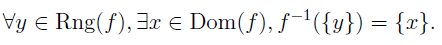
Summary:
- function is the most useful abstraction in mathematics
- function is a special type of a binary relation,
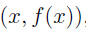 , with an input and a corresponding output
, with an input and a corresponding output - a function has a domain, a codomain and a range.
- functions are tied up to the rule that give the output and the type of input (domain) given
- a function is surjective if every element of the codomain has a preimage
- a function is injective if its preimages are unique
- a function is bijective if it is surjective and injective
- the inverse of a function is simply formed by exchanging the elements of the ordered pairs y=x
- the ideas of images and preimages can be extended to sets
Disclaimer: this is a summary of section 6.5 from the book A Gentle Introduction to the Art of Mathematics: by Joe Fields, the content apart from rephrasing is identical, most of the equations are screenshots of the book and the same examples are treated.
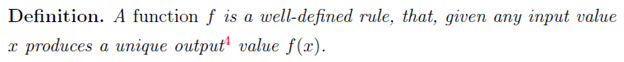

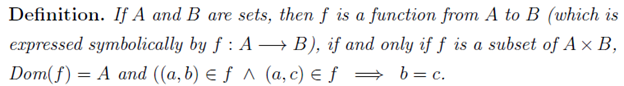
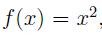
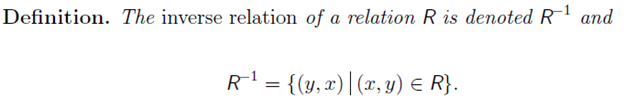



Thank you for your post. :) I have voted for you: 🎁! To call me just write @contentvoter in a comment.