A Gentle Introduction To Mathematics - Counting
Counting
Many questions in Mathematics are related to the question: “How many … “?
- How many subsets does a finite set have?
- How many handshakes will transpire when n people first meet?
- How many functions are there from a set of size n to a set of size m?
What we aim is to be able to count some collection in principle so that we will be able to discover a formula for a size. This is a useful relation in combinatorics,

But first, we will consider the simple counting technique to get the idea how we reach to that equation. Consider the following,
A method that does lead to a generalized ability to count the elements of a finite sequence arises if we think carefully about what exactly a finite sequence is.
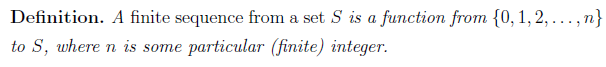
It is easy to see that there are n+1 elements in the set, so counting the elements of a finite sequence will be easy if we can determine the function involve and figure out what n is by inverting it.
Generally, if there is a list of consecutive numbers beginning with k and ending with n, there will be n-k+1 entries in the list.
There are two principles that will be useful in counting things.
- Multiplication rule which tells us when we should multiply
- Addition rule which tells us when we should add
We’ll examine the principles by looking at some examples.
Addition Rule
The addition rule says that it is appropriate to add if we can partition a collection into disjoint pieces. So if S is a set that is a union of two or more subsets, then we can find the size of S by adding the sizes of the subsets.
Multiplication rule
Multiplication rule gives us a way of counting things by thinking about how we might construct them. The numbers that are multiplied are the number of choices we have in the construction process. A very important assumption one should remember is the independence of the number of choices we can make in a given stage of constructing some configuration to the choices that have gone before.
If a configuration can be realized in k stages, and if the first stage we have n1 choices as to how to proceed, n2 choices in the second stage, et cetera. Then the total number of such objects is the product 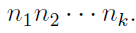
Permutation:
A permutation of an n-set is an ordered n-tuple where each entry is a distinct element of the n-set.
1. n-set Permutation
Let’s calculate the permutations of 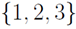 . The permutation of this set will be a 3-tuple containing the numbers 1, 2, and 3 in some order.
. The permutation of this set will be a 3-tuple containing the numbers 1, 2, and 3 in some order.
There are 3 stages to build this permutation:
- Select a number to go in the first position – there are 3 choices for this
- Now, the second position will be limited to two possibilities only
- Finally, there is just one number remaining to put in the third position
Thus there will be a total of 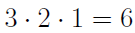 permutations of a 3 element set.
permutations of a 3 element set.
General rule: for a set 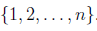 there will be n! permutations.
there will be n! permutations.
There are instance where we want a configurations but don’t consist of all n numbers at all.
2. k-permutation
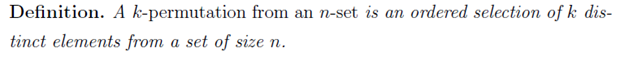
For the variable k, it is assumed always to be positive, and less than n: 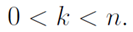 The notation
The notation 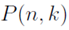 is used for the total number of k-permutations of a set of size n.
is used for the total number of k-permutations of a set of size n.
Building k-permutations is achieved easily using multiplication rule in k stages.
- Stage 1, the first element in in the permutation has n possible choices
- Stage 2, we pick the second element, now we have (n-1) possible choices since we may not repeat the first entry
- We keep doing this until we’ve picked the k entries.
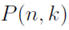 is then the product of k numbers beginning with n and descending down to (n-k+1).
is then the product of k numbers beginning with n and descending down to (n-k+1).
Example:
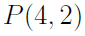 is 12 since (4*3 = 12)
is 12 since (4*3 = 12)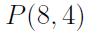 is 1680 since (8x7x6x5=1680)
is 1680 since (8x7x6x5=1680)
To simplify the calculation of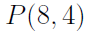 we use factorial. The general rule is given as
we use factorial. The general rule is given as
3. n-set’s k-combination
A k-combination from an n-set is an ordered selection, without repetitions, of k things out of n. The set is a subset of size k of a set of size n, and the number of elements in this subset is denoted by several notations:
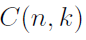
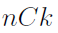
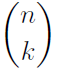
The k-permutation is related to k-combination by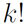
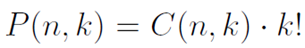
From our previous definition of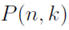 , we substitute to the equation above and solve to obtain
, we substitute to the equation above and solve to obtain
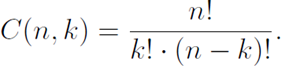
Four Types of Counting Problem (Ordering and Repetition)
The counting problem can be partition into four types based on the following questions
- Is order important in the configurations being counted? (Ordering)
- Are we allowed to have repeated elements in a configuration? (Repetition)
It is best to explore this idea of ordering and repetition with examples.
Ordered with repetition
PIN number of a bank account is a good example of a kind of problem that put importance on the ordering and repetition of numbers. A PIN number of 1356 is different from a PIN number of 6531. For security purposes, repetition of numbers is avoided. For instances a PIN like 3333 is easy to guess. But people are free to choose whatever PIN number they wish.
A PIN number is a 4-tuple item whose elements are from 10 numbers where repetition is allowed. There are 10 choices for the first digit, 10 choices for the second digit, and then still 10 choices for the third and fourth digit as well. This gives us a total of 10x10x10x10 = 10000 configurations.
Generally, out of n possibilities selecting k things where order and repetitions are allowed there will be 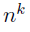 possible selections. In the PIN account example, n =10 and k = 4.
possible selections. In the PIN account example, n =10 and k = 4.
Ordered without repetition
Think of a password for a computer account. Chances are it is consist of letters (52), numerals (10) and symbols and punctuation marks (32) – that a total of 94 characters used. Now, suppose your account requires 8 characters and will reject a password that has repeated symbols.
How many passwords are possible?
The multiplication rules tells us that there are 94x93x92x91x90x89x87= 4488223369069440 different passwords. We’ve actually just calculated the 8-permutations of n=92.
In the general case, selecting k things out of set of size n, without repetition and with order counting there will be 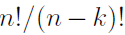 possibilities, also denoted by
possibilities, also denoted by 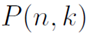 .
.
Unordered without repetition
How many different sequence of 6 strictly increasing numbers can we choose from 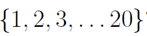 ?
?
We’ve already discussed this previously. Again, if we are choosing k things out of n and order is unimportant and there can be no repetitions, then we are describing a k-subset of the n-set. There are
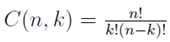 distinct subsets.
distinct subsets.
The number of sequence is C(20,6)=38760 but this is strictly an unordered selection without repetition. But we note we were asked to consider a strictly increasing sequence of numbers, hence requiring that our set be ordered. There is clearly something wrong with using C(20,6) since it involves unordered collections.
Interesting, by imposing a strictly increasing sequences we are actually removing the importance of order; that is, given the symbols 1 through 6, we could put that into 720 different orders but there is actually just a single sequence that is increasing.
There is a one-to-one correspondence between a 6-subset of 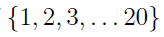 and a strictly increasing sequence.
and a strictly increasing sequence.
Unordered selections of k things out of n possibilities where there may (or may not!) be repetitions
Yahtzee provides a good example for this type of configuration. The outcomes in Yahtzee are 5 numbers from the set 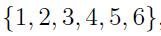 . No repetitions are possible, however repetition of two numbers on two or all five of the die are also possible.
. No repetitions are possible, however repetition of two numbers on two or all five of the die are also possible.
How do we express the outcome when we roll the five dice at the same time?
We can do this by manually listing all the possible configurations but this time, it would be better if in an increasing order.
First, we start the list with some number of 1’s then there are some 2’s, then some 3’s then some 4’s then some 5’s and finally some 6’s.
We can count something related to the problem above in a simpler manner using blank-comma arrangements. For the Yahtzee problem, we count arrangements of 5 blanks and 5 commas.
Summary
Now that we’ve completely explored all the types of possible counting restrictions we can produce, our table of counting formulas is as follows. (We’ll shift from the old notation 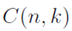 to a new notation on the k-combination
to a new notation on the k-combination 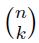 , commonly used as “binomial coefficient”. )
, commonly used as “binomial coefficient”. )

Disclaimer: this is a summary of section 7.1 from the book A Gentle Introduction to the Art of Mathematics: by Joe Fields, the content apart from rephrasing is identical, most of the equations are screenshots of the book and the same examples are treated.


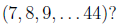
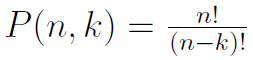
You got a 2.40% upvote from @emperorofnaps courtesy of @sinbad989!
Want to promote your posts too? Send 0.05+ SBD or STEEM to @emperorofnaps to receive a share of a full upvote every 2.4 hours...Then go relax and take a nap!