[Apostol's Calculus] Exercises 1.5: Solution to 14
Assume f is in S, and has the additive inverse (axiom 6) g such that f + g = 0. Then the primitive of f, F(x) satisfies the property:
F(1) - F(0) ≥ 0.
This implies that F(1) ≥ F(0), so f(x) must be greater than zero, since f(x) is the derivative of F(x), and F(x) must be increasing.
At the very least, (f(1) + f(0))/2 ≥ 0 (the average slope of the primitive must be positive or zero)
But this must also hold true for g and its primitive G, since g is also an element of S. But if f ≥ 0 and g ≥ 0, then (f + g) ≥ 0. The only (f + g) = 0 is if f and g are both zero, since neither can be less than zero.
QED
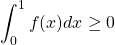
@OriginalWorks