A mathematical riddle
Imagine there is a disease that afflicts just 1 in every 100 people in the population. A new test has been developed to detect the disease that is 99% accurate. That is, for people with the disease, the test correctly indicates that they have the disease in 99% of cases. Similarly, for those who do not have the disease, the test correctly indicates that they do not have the disease in 99% of cases.
If a person takes the test and the result of the test is positive, what is the probability that he or she actually has the disease?
I look forward to your responses :-)
P(A|B) = .99 * .01 / [(.99*.01)+(.01 * .99) = .5
or 50% ?
Very good!
:) woots!
99.01% chance?
99% accurate test, +.01% chance for potentially being one of the hundred afflicted?
Not entirely confident in my answer, math isn't my forte. Figured I would give it a shot though.
Sadly, it's a bit more complicated. You have to use the Bayes's theorem:
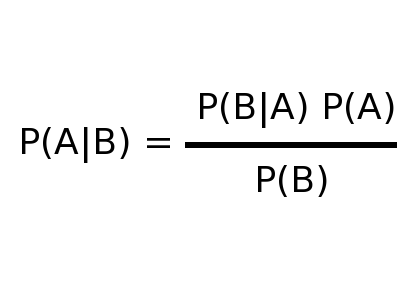
In the denominator it is the unconditional probability of a positive test (the probability of being tested positive if having the disease + being tested positive if not having the disease --> 1%99%+99%1%). I hope this helps.