Percentages will and should probably be the most used mathematical tool in your personal finances. Next to Addition, Subtraction, Division and Multiplication, calculating Percentages should be very important for your financial management.

Whether you are counting how much profit a dividend will pay you, or how much taxes you need to pay, or how much your bills went up, it is nearly impossible to do these things correctly without understanding how percentages work.

---

WHAT IT IS

A percentage is technically a form of differencing or differentiation, which means to take the difference between 2 numbers. Of course subtraction is also a form of differencing, but that is additive, a percentage is a multiplicative form.

In some cases or financial models an additive difference is better:

• Ex: Calculating your rent cost changes. You might not care about how much percent it went up, but if it went up by 10$,20$,50$ or so
  In other cases a multiplicative model is better, use percentage:
• Ex: You calculate how much % the taxes increased, and not necessarily care about the amount, since it depends on the % of your revenue
  
  

FLAWS

Now you might think calculating a percentage is easy, just take:

NEW_VALUE/OLD_VALUE*100

Of course as simple as it sounds, it has some serious mathematical flaws, first of all:

• It's not Time additive:

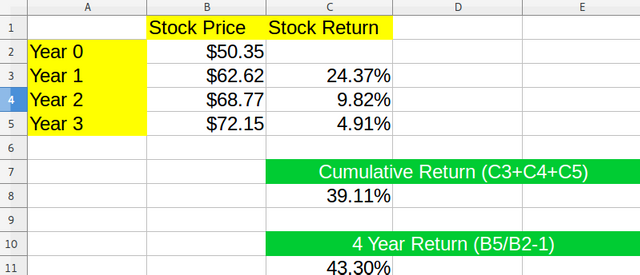
When calculating returns, we also subtract 1 from it, and convert it to percentage by multiplying by 100. We use Excel or LibreOffice and it's easy to calculate. Above I have demonstrated why it's not time additive.

If we calculate the returns separately, and add them up, it won't be the same as if we take the first and the last value and calculate it's returns. It should be, but it's not, this is the flaw of the percentage. It has this compounding effect to it, that is sometimes inaccurate.

So in reality real scientists prefer to not use percentages often, because this small flaw could ruin many calculations.

LOG DIFFERENCE

It's based on the natural logarithm, or ln(x). The log returns are time consistent, so the problem that we see with the percentages vanishes.

To calculate a natural logarithm you have to do this:

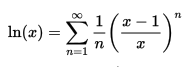
But since we are blessed with spreadsheet softwares, we just type in ln(x) and they do the hard work. To calculate a log return simply do:

LN(NEW_VALUE/OLD_VALUE)*100

The difference is inside the log function, and it sort of standardizes it, so while a percentage is not giving the same results for it's derivations, the log return or log percentage does:

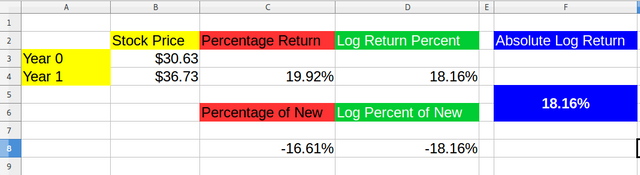
We can see that the log return is standardized, and it's the same absolute distance in both way, both A/B as B/A will give the same result except the negative sign, but the absolute value will be the same. Whereas in percentages it differs significantly.

This characteristic of standardization is what gives it's value, and it's much easier to work with it, and not have to think about the order of variables, just use the absolute value.

It is also time consistent, both added up logs, as bigger distance logs will add up the same:

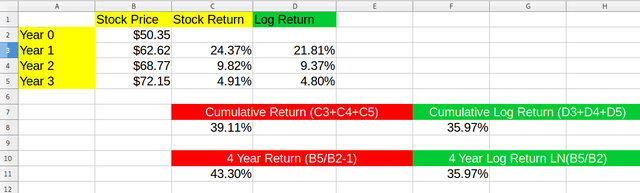
In my opinion everyone should use the log difference whenever calculating financial returns, to give you a more robust and accurate difference between your 2 datapoints.

---

Disclaimer: The information provided on this page might be incorrect. I am not responsible if you lose money using the information on this page! This is not an investment advice, just my opinion and analysis for educational purposes.

Credits: https://www.wikipedia.org

---