Roulette is one of the most popular casino games. In this article we will examine the math behind the game, and the probabilities of winning.

Roulette in French means "little wheel", it is a wheel based game, where you can bet on numbers and the properties of the numbers that will be chosen by the wheel.

Needless to say that the game has negative expectancy, regardless of the "strategy" you use, so you will probably lose through the longterm, however if you are "lucky" you can go away with some winnings in the short term.

There are major 2 variants, the European with 37 numbers and a house edge of 2.702702697% and the American version with 38 numbers and a house edge of 5.263157853%. There are also wheels with double-zero, and with single zero.

In this analysis we will look at the European version since it's "easier" to win with a smaller house edge. The green square with the 0 gives the house edge, since it imbalances the bets for example the black/red bet would have a 50-50% probability without the green 0, but with it it has a probability of win of only 48.648648649%. A 50-50% probability would still not result in a profit over longterm, since the profit will converge to 0, but with a negative house edge it converges to a loss, rather exponentially.

You can only win consistently if the expected value is higher than 0, but no gambling game offers that, since the casino would go bankrupt instantly. Instead gambling is just an entertainment game, and people should not look for it to get rich quick.

---

Playing

It doesn't matter how you bet, the expectancy is the same, only the probability - payout is skewed a little bit. For example betting on single numbers offers a larger payout, but has a small probability, but the expectancy is the same. For simplicity we will only talk about betting on colors: red/black in this example.

Betting on color gives exactly the 50% - house edge/2 probability. There are 37 numbers, 36 are colored, 1 is the zero. You have a probability of winning of 18/37, and a probability of losing of 19/37.

So it's 48.648648649% for black and 48.648648649% for red, and an extra 2.702702703% for the 0 ball, which is exactly the house edge (that skews it into negative EV), together it makes up 100%.

PROBABILITY OF WIN = 50% - HOUSE EDGE / 2

The payout in the European roulette can be calculated with the following formula:

PAYOUT = 36 / SLOTS - 1

Which in our red/black bet case, is 36/18-1 = 1. This means that you get back exactly 1x your bet if you win, or the odds are 2x, while the probability is what it is, shown above. So let's put it all together and see the EV:

EXPECTED VALUE = PROBABILITY_OF_WIN * PAYOUT - PROBABILITY_OF_LOSS

So this means that in our case we have a probability of win of 48.648648649%, and a probability of loss of 51.351351351%. If we bet red/black, with 1$, then our EV is:

EXPECTED VALUE = 48.648648649% * 1 - 51.351351351% = -2.702702702%

It is exactly the negative of the house edge, because obviously what the house wins, we lose, longterm. So then we just calculate the profits, which is multiplied by our betsize & number of bets:

PROFIT = EXPECTED VALUE * BETSIZE * NR_OF_BETS

For example if we play 100 roulette games with a bet size of 10$, then we should expect to have at the end:

PROFIT = -2.702702702 * 10 * 100 = −2702.702702 $

A profit of −2702.702702 $, very very profitable, what can I say. But of course this is the convergence value, if your bets converge towards the probability, but this is not always the case in a small sample size like 100 bets. You can have consecutive wins and losses, so it's all random, you cannot know what your profit will be, but it should converge towards this value.

---

Conclusion

Yes gambling is not profitable over the longterm ,because your profits will converge to the negative EV eventually, which means that you will lose money no matter what. But that doesn't mean that some gamblers could not get lucky and win something short-term. But most of you won't win, that is the key, it's all a game of randomness, and whoever is lucky wins something, but if they don't stop, then they will lose it all. So gambling should not be a business model for you!

It's the law of large numbers, numbers always converge towards their mean, and in this particular case the mean is negative so your profits will too be the same.

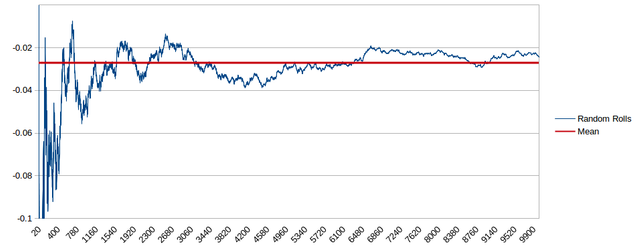
Here is a simulation on 10,000 bets, as you can see the mean is the house edge -0.027027027, however the bets deviate a little bit, in a normally distributed way (it's all random, but the distribution is normal), but they converge towards the mean over a long period of time:

---