Crash course in mathematics: Lesson 5 - Little Gauss

This lesson is about mathematical thinking. If it is the first lesson of this crash course you encounter, or you missed some lessons, please go back to the beginning and follow the course trough, by using the framework and index, at the end of the introduction

---

The year is 1785. The place, an elementary school class in Brunswick, lower Saxony. Eight years old Gauss is bored. According to his own testimony later in his life, what his fellow pupils were then struggling to understand, he already figured out before he could walk. The teacher wants to get the little math prodigy to do something, so that he will not disturb the other pupils, so he asks Gauss to go to the board and sum up the numbers between 1 and 100. To his surprise, Gauss comes up with the answer after just a short moment ( it is 5050 ).

Now, you may have heard of people who can do such calculations, and even more complicated ones, very fast in their heads, but that is not what little Gauss did. Instead, he noticed a principle, which allowed him to make a much simpler calculation. What little Gauss saw is this:

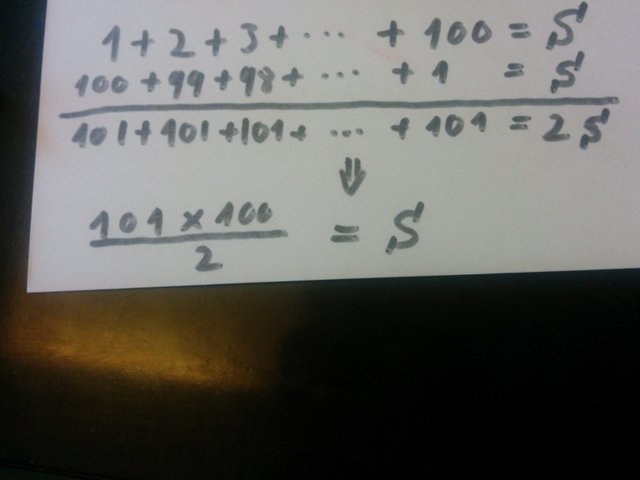
Now let’s try to tap into the mind of a mathematician who solves this kind of problem:

I don't know what the sum of the numbers 1 to 100 is, but I can still give it a name. Let's call it “S”.

Names are very important in mathematics, because once something is named, it becomes a thing that can be manipulated in certain ways, without us having to wonder about its exact attributes or meaning, that is as long as we understand that we mean the same thing. In math, it is not a good idea to have three Marys, like in the Christian gospels.

OK so now I have an equation. Let's see what other equations I can infer from it…

We will have a whole lesson, maybe even more than one, dedicated to equations - one of the most misunderstood mathematical concepts, but at this point I just want you to observe how every time mathematicians see an equation, they immediately start looking for other equations that can be inferred from it.

What would happen if I add the numbers, from the end to the beginning? Oh, that's interesting! The sum of each number in the series and it’s counterpart when adding the series backwards, is always 101!

Now why did Gauss decide to add the numbers backwards , of all things? Well, like one of my teachers in the University used to say, “Well, that's because he was Gauss!”, but to be more specific, this is one of many examples in the work of Gauss of how he used predictive thinking, not just analytical thinking, to solve mathematical problems. Predictive thinking is not magic or prophecy. It is actually the habit of taking what you already know and dare using it to consider new possibilities. It is a combination of courage and reasoning, with the reasoning part being responsible for considering your options in a certain order, and carefully checking if they are valid or not.

I told you that this is a basic swimming course. But that doesn't mean that we can't sit on the shore and tell stories about those who dared to imagine, that there is something beyond the horizon. In the next lessons, we will start learning the very basic stuff. But always remember that it can take you much further than you may think.