About the sequence 1, 11, 21, 1211, 111221, 312211, ...

Consider the beginning of the following sequence:

1, 11, 21, 1211, 111221, 312211, 13112221, ... .
Could you find the next term and the formation rule of the sequence?

Before you continue reading, you should stop reading and think about this problem for a moment.

Let us start with the first term:

"1", What do you see? The answer is "one 1", you can put it differently as "11".

So the next term of the sequence is "11". What do you see now? "two 1s" that is "21".
This term is read as "one 2 and one 1", that is "1211", the fourth term of the sequence.

Now "1211" is read as "one 1 one 2 and two 1s", that is "111221". If you read this term is "three 1, two 2s and one 1", or "312211", the sixth term of the sequence.

Have you grasp the idea of the formation rule of the sequence? If so you can say the eight term of the sequence is "1113213211".

For this reason this sequence is known as look and say sequence and it was introduced by the British mathematician John Conway in 1986.

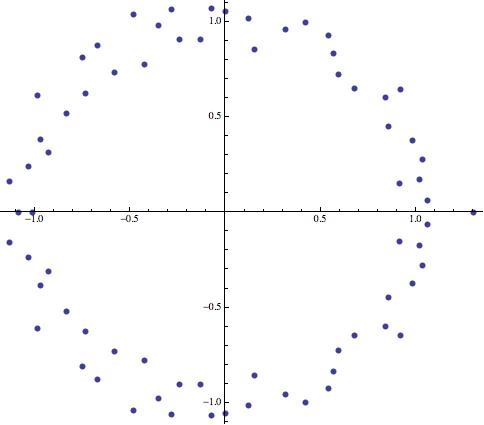
Roots of the Conway polynomial, plotted with Mathematica.

You might think that this is a mathematical joke. Well, it started like a joke, but we can say some interesting things about this sequence from the mathematical point of view. We can ask different questions, among them:

• Besides the numbers 1, 2 and 3, Do other digits appear in the sequence?
• What is the growth of length of the general term of the sequence? This means the following, consider the n-th term of this sequence and denote by D_n the number of digits that has. For example: D₁=1, D₂=2, D₃=2, D₄=4, D₅=6 and so on.

We would like to know the growth rate of D_n, i.e.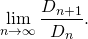

The answer of the first question is negative. It can be proved that besides the digits: 1, 2 and 3. no other digits appear in the terms of the sequence.

The answer of the second sequence was also given by Conway. This limit exist and today is called the Conway constant and its value is approximately 1.303577269034... It is the only positive real root of the following polynomial of degree 71, called the Conway's polynomial:

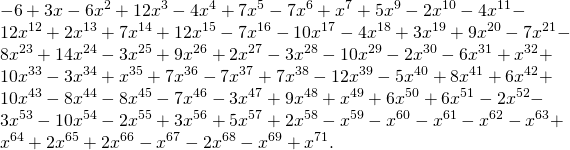
The roots of this polynomial can be seen in the figure as blue dots.

A more sophisticated analysis of this sequence can be done.

References:
https://en.wikipedia.org/wiki/Look-and-say_sequence
https://oeis.org/A005150
https://oeis.org/A137275
http://mathworld.wolfram.com/LookandSaySequence.html
J. H. Conway, The weird and wonderful chemistry of audioactive decay, Eureka 46 (1986) 5-16.

The image of the roots of the polynomial was done by myself using Mathematica and the polynomial formula with LaTex.