Every triangle is equilateral
Every triangle is equilateral
Here is a small proof of the equality "2=1"
- Choose two numbers a and b such that a=b
- Multiply by a to get : a²=ab
- Substrating b² gives : a²-b²=ab-b²
- Factoring by a-b gives : (a-b)(a+b)=(a-b)b
- Divide by (a-b) to get a+b=b
- Finally, choose a=b=1 to get 2=1
In this "proof", the trick is not really well hidden : if a=b=1, then we shouldn't be allowed to divide by a-b as it would be zero.
In this post I'll be presenting a "proof" of the obviously fake assertion that every triangle is equilateral. The flaw in this proof is not easy to find and I'll leave it as a challenge to find it, or give it on request in the comments.
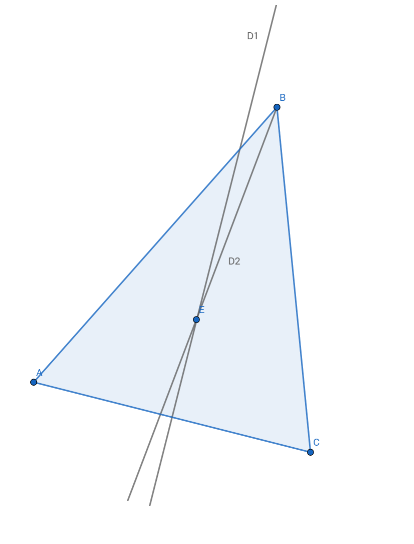
Angle bisector and segment bisector
Take a triangle ABC and draw the angle bisector of the angle in B, and the segment bisector of [AC]. They intersect at a point named E.
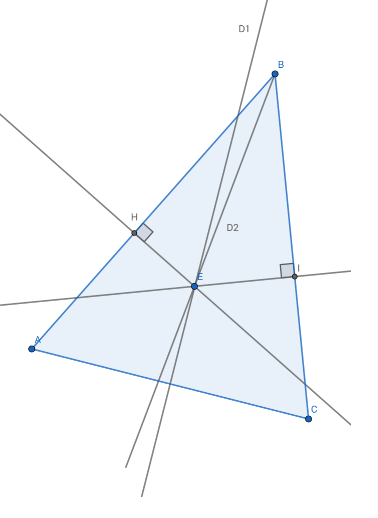
Project the point E on the two segments [AB] and [BC], and get two new points, H and I
The reasoning is the following :
- D2 being an angle bisector, and E being on D2, the lenghts BI and BH are equals, as well as the lenghts EH and EI
- D1 being a segment bisector, the lenght EA and EC are equals.
- The triangles AEH and ECI have two pairs of equal sides (EI=EH and EC=EA) and the angles EHA and EIC are equal because they are both right angles. Thus, the triangles AEH and ECI are equal, and it gives the equality HA=IC
- We have proven that BH=BI and that HA=IC, and the sum of these equalities gives BA=BC, proving that ABC is an isocele triangle. Repeat the proof on one other side to conclude that the three sides are equals and that ABC is an equilateral triangle.
Can you find the flaw in this proof? Feel free to leave a comment to share your answer or ask for hints !