Intuitive Math: Everybody Can Understand Complex Numbers Part 1: It's all about rotation
When complex numbers were first introduced in school most people hated them. There was seemingly no intuition about them and they were considered complete nonsense. While the teacher could give no plausible justification for their existence, he promised that they will play a big role in higher mathematics later in university. And then when you came to university, they were suddenly everywhere, yet, when you asked the lecturer what they actually represented, he told you they were basic knowledge and sufficiently introduced in school. But he would also add that you didn't have to understand them to excel in the exam. "Simply use the formulas" he said.
Ok, now let me give you a very intuitive explanation about what complex numbers are and (why they are so beneficial - Part 2).
If you aren't at all familiar with complex numbers you may want to read this excellent Steemit post about complex numbers from krishtopa.
Well, now you know that complex numbers are two dimensional and that you can sketch them as vectors into a coordinate system and that they can solve the following equation:
But what does that mean? It seems like an arbitrary definition. So let's first take a look at a mathematical operator everyone knows: multiplication by -1.
If you have positive number and multiply it by -1 it basically just flips it by 180°
(these two figures are from krishtopas post)
That's why minus times minus equals plus (double flip = 360°). With rational numbers you can not solve the equation x^2 = -1 because you can never have two 180° flips and end up flipped 180° ;)
So now what does the complex operator i do? How does it solve this problem? As we want to end up flipped 180° the i operator rotates it by 90° twice. And that's all what it does it rotate your number by 90° instead of 180° giving you a two dimensional representation. Here is the complex number i:
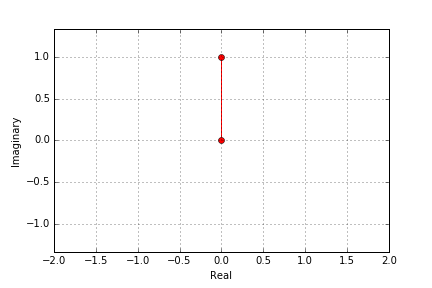
But we can not only represent a 90° rotation, but any arbitrary rotation angle e.g. 1 + i:
Ok, if you're a bit familiar with complex numbers you already know that and that's why I don't elaborate here. The only thing we have to remember is that i is a rotation operator.
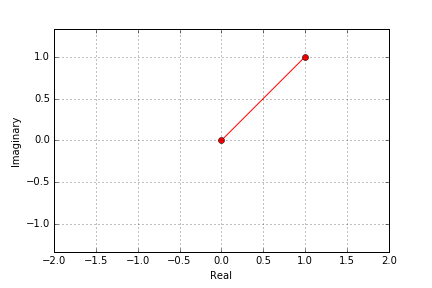
No let us bring up another mathematical concept: continuous growth. If you have a plant and assume that it grows in one big burst 5% per year you could express that by (Initial Plant Size) * (1 + 0.05). But well that's pretty unrealistic for the plant to do nothing for 364 days and then suddenly explode growth. So we now say it grows 12 times a year in more tiny steps which would mean (Initital Plant Size) * (1 +1.05/12)^12). But that's still not what's happening because a plant grows continuously (infinitely often infinitely small steps) so we can generalize:
We all learned that continuous growth is exponential growth and that's why
So continuous growth with real numbers can be easily represented and dealt with. Now comes the interesting part. What happens if we grow complex numbers in the same way. So we just take a complex number e.g 1 + i/10 and do the imaginary growth (both scaling and rotation) like
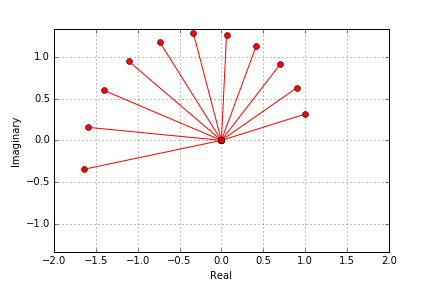
I just wrote a small python program to illustrate this
What we see is that the complex vector is rotated with increasing length spiraling outwards. Now let us take a look at continuous complex growth.
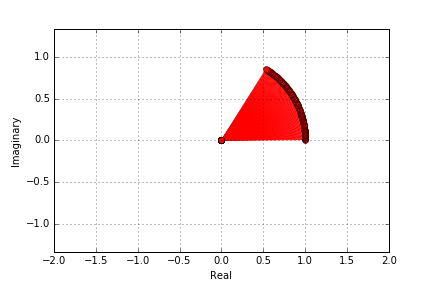
For practical purposes I choose n = 100 as it is an sufficient approximation and for x = 1 I get the following:
So, we are beginning to see part of a circle with a radian measure of 1 (circumfence of the circle segment)
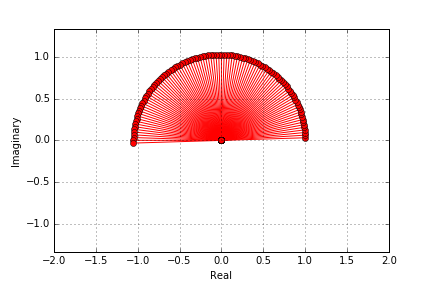
What happens if we set x = Pi. Again n = 100:
How cool is that? We get a semicircle. Can you guess what happens for x = 2*pi or x = pi/2? We just found an amazing way to represent a circle with e and the complex number operator giving us the common polar form of complex numbers.
We just plug in the angle and rotate the complex vector by exactly that angle while the length is preserved. So putting in 2* Pi gives us a full circle and pi/2 gives us a quarter circle.
So now it's just super easy to understand the most beautiful formula in all of mathematics:
It's just a specific expression of our 180° flip operator while we can now with our polar form perform any arbitrary rotation. Easy isn't it?
If you like this concept and want to see how this greatly simplifies practical applications in science upvote, comment and follow me @mcsvi.
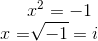



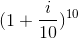
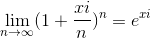
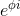
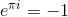
Nice approach to this fascinating subject.
Maybe you will enjoy this 10 minute video:
https://steemit.com/mathematics/@point/imaginary-numbers-breakthrough-to-reality
You did an excellent job!
This is a really great post! Thanks for taking the time to make this, I truly appreciate it!
Wow, this is amazing. Finally there is a guy that saw the beauty of abstract notions from the math area. It seems you're passionate about math. Niiice.
Thank you. I'll follow you, of course.
Thanks. Yeah, I quite like breaking down those mysterious math concepts ;)