Introduction to Geometry (Level 5) | Sets, Union, Intersection I
Introduction to Geometry (Level 5) | Sets, Union, Intersection I
In this post we are going to go over basic examples that ask us to find the intersection and union of various geometric figures. Before we jump into some examples lets refresh our memory and talk about sets. Say I have two distinct sets let’s call them Set A and Set B.
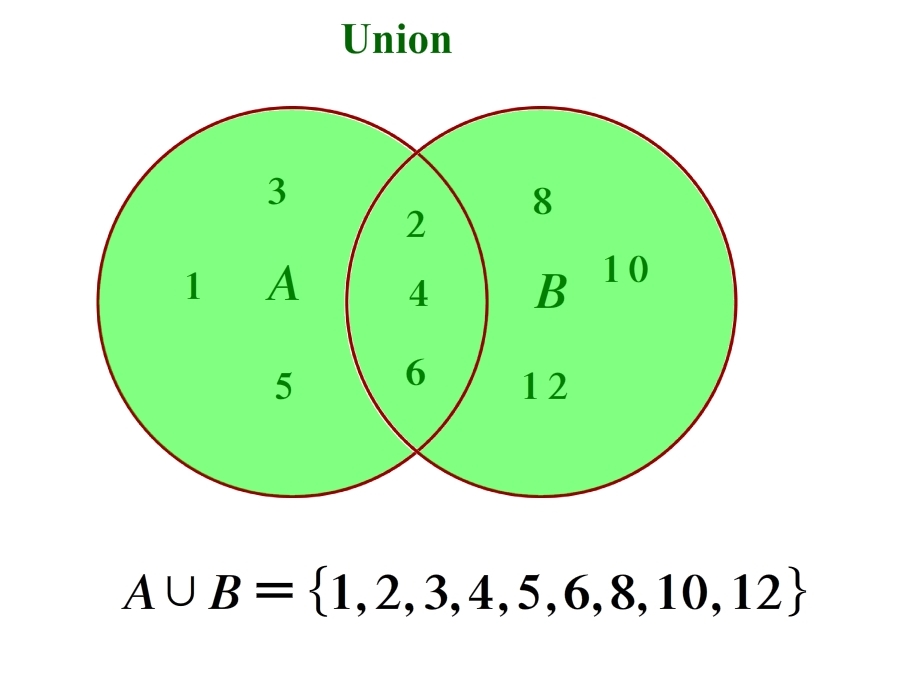
Recall that a set is a collection of objects, these objects are referred to as the elements of the set. In this example the numbers 1,2,3,4,5,6 are the elements of set A, likewise the numbers 2,4,6,8,10,12 are the elements of set B. When dealing with sets we are often asked to find the union or intersection between two or more sets.
If we are asked to find the union between set A and B we would denote it as follows:
This symbol is pretty easy to remember since it looks like the letter U for union. In essence, the union between two sets consists of all the elements in A or in B or in both. You can think of a union as the process of merging the elements of both sets together.
In this example A union B will be equal to a new set that contains every element that is in either set A or B including those elements that are common to both set A and B.
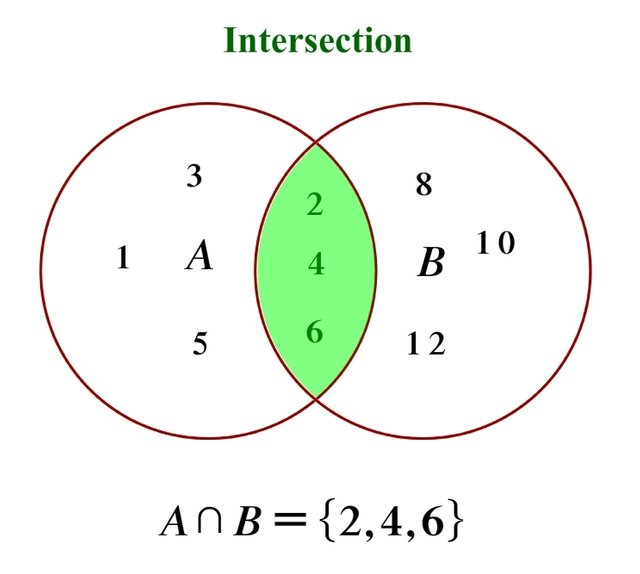
In contrast, if we are asked to find the intersection between set A and B we would denote it as follows:
This symbol looks like an upside down U and it sort of looks like the capital letter A if you use your imagination, you can imagine the capital letter A to remind you of the word “and” since the intersection of two sets creates a new set containing the elements in both A and B. In this example A intersected B would equal to the set containing the elements 2,4 and 6 since these elements are in both A and B, graphically you can see the reason why this is called the intersection between two sets its literally an intersection or overlapping of common elements.
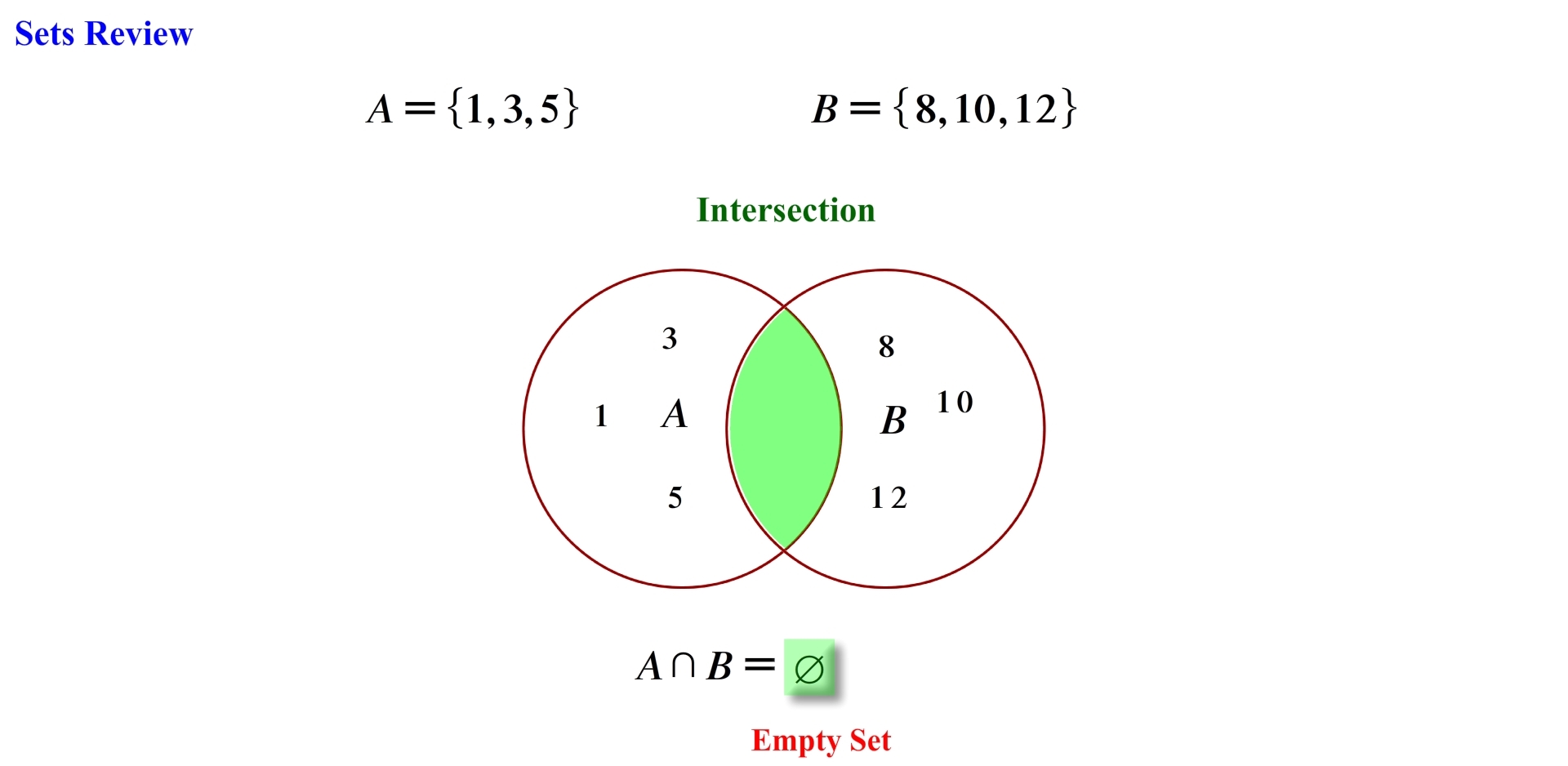
The final concept we need to be familiar with is the idea of an empty set, let’s take Set A and Set B and remove their common elements.
Now if we are asked to find A intersection B we would see that there are no common elements between set A and B, in this case we would obtain what is referred to as an empty set, and we use this symbol to denote an empty set, an empty set contains no elements.
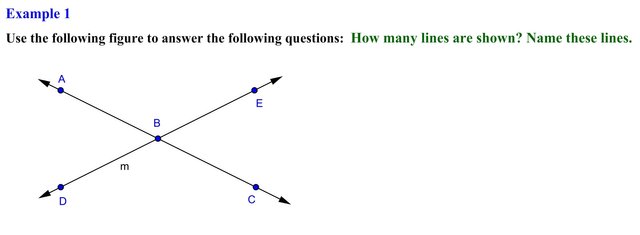
Alright now that we are refreshed and familiar with the concepts associated with sets lets go ahead and try the first example.
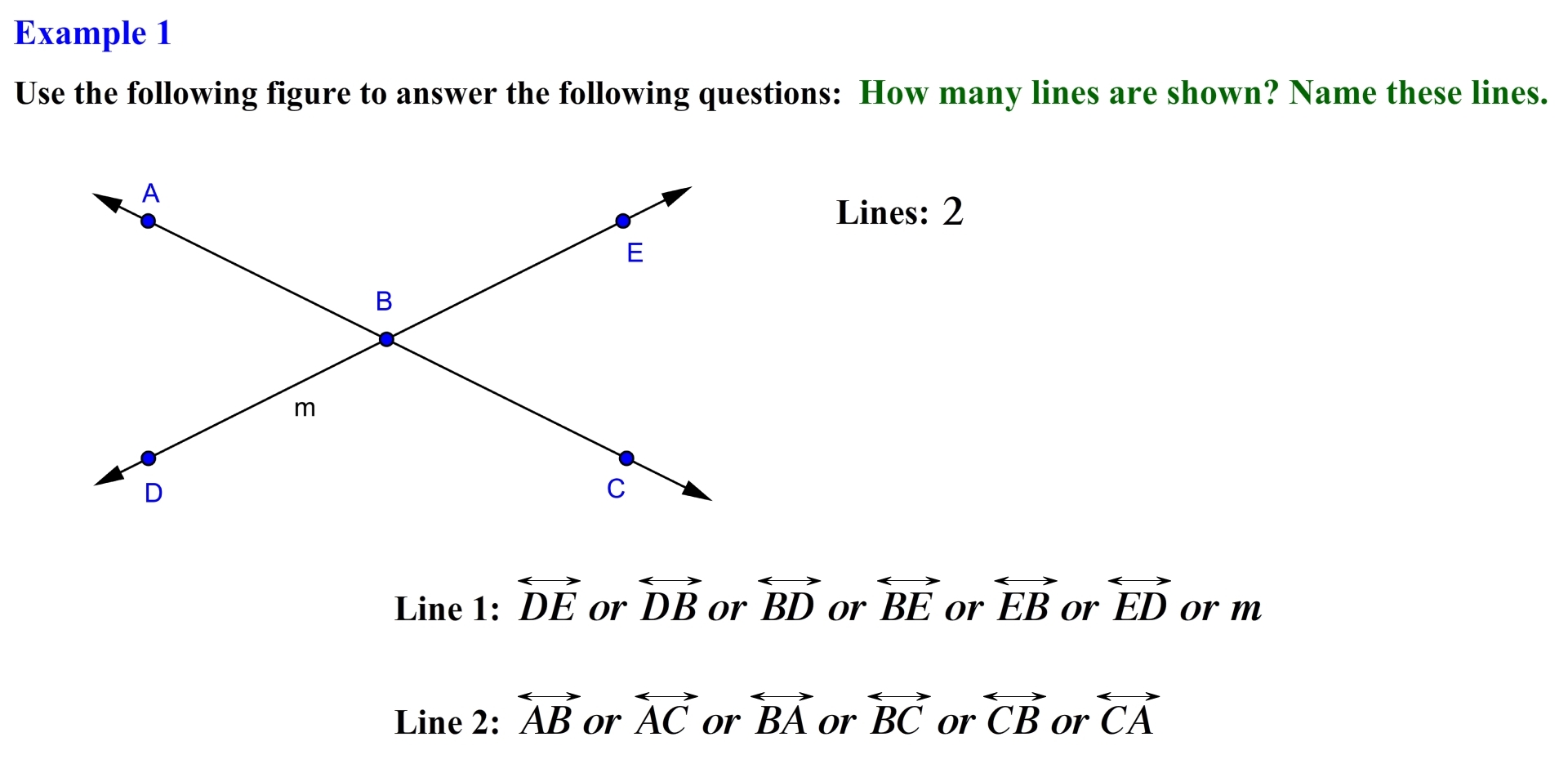
By looking at the figure we can see that there are two distinct lines. So the answer to the first question is 2. Now the second question is asking us to name them, let’s focus on the line that contains points D, B and E, this line can be named by using two points so we can name this line as line DE, DB, BD, BE, EB, or ED, notice that this line is labeled with the lower case letter m, so we can also name this line as line m. In the same manner, the line that contains points A B and C can be name as line AB, AC, BA, BC, CB or line CA.
Remember lines can be named by denoting two points on the line or by using a lower case letter whenever possible. Alright, let’s try the second example.
Using set notation this problem translates to the following expression:
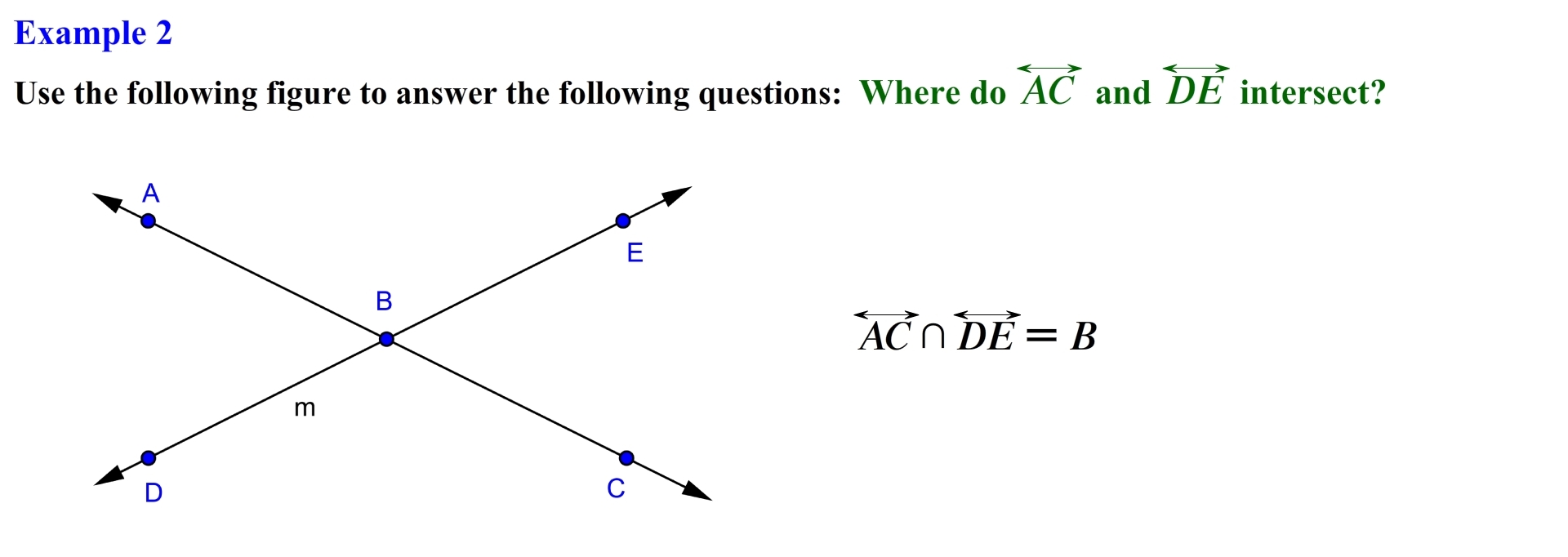
Looking at the lines we see that they intersect at a common point in this case point B. so line AC intersection line DE is equal to point B. Let’s try the next example.
Using set notation this problem translates to the following expression:
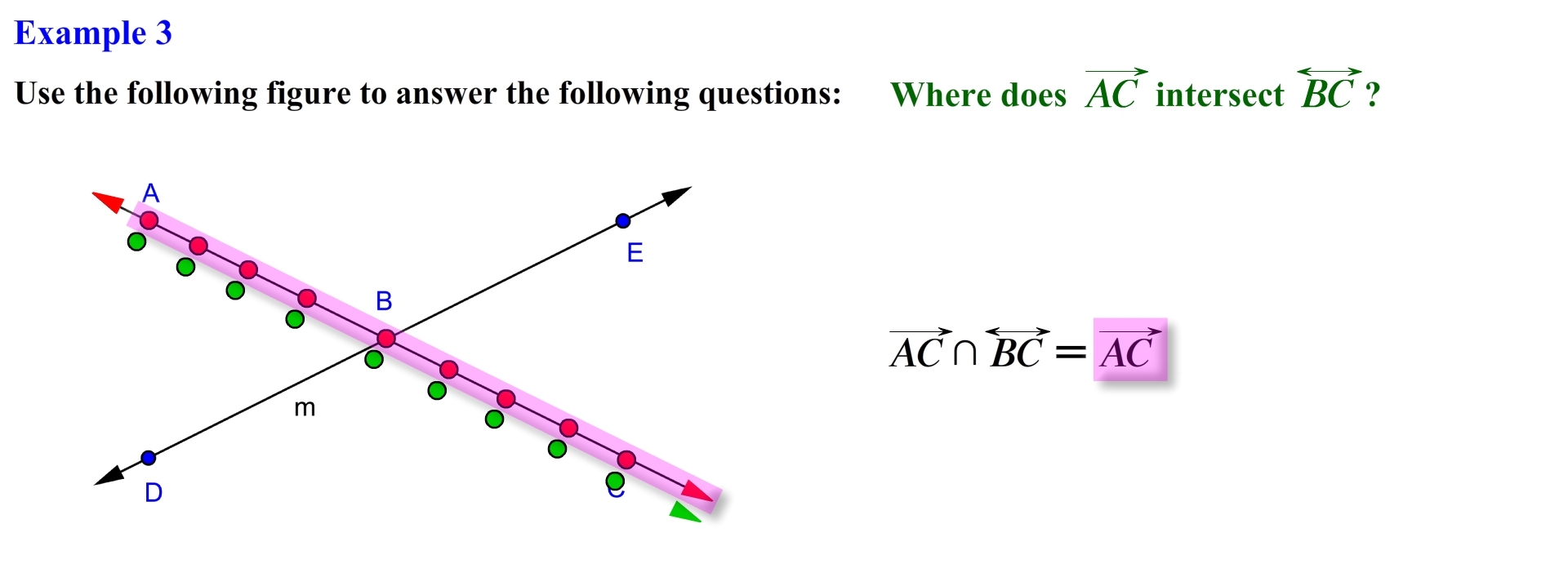
Recall that you can think of a ray as being the set of all points that starts at one end point in this case point A and goes in the direction of another point in this case point C, in the same manner a line is the set of all points that extends infinitely in both directions so the following points are located on line BC, for this problems we are looking for the points that both ray AC and line BC have in common hence the intersection, in this case the common points start intersecting at point A and extend infinitely in the direction of point C, therefore the intersection of ray AC and line BC is equal to ray AC. Let’s try the next example.
Using set notation this problem translates to the following expression:
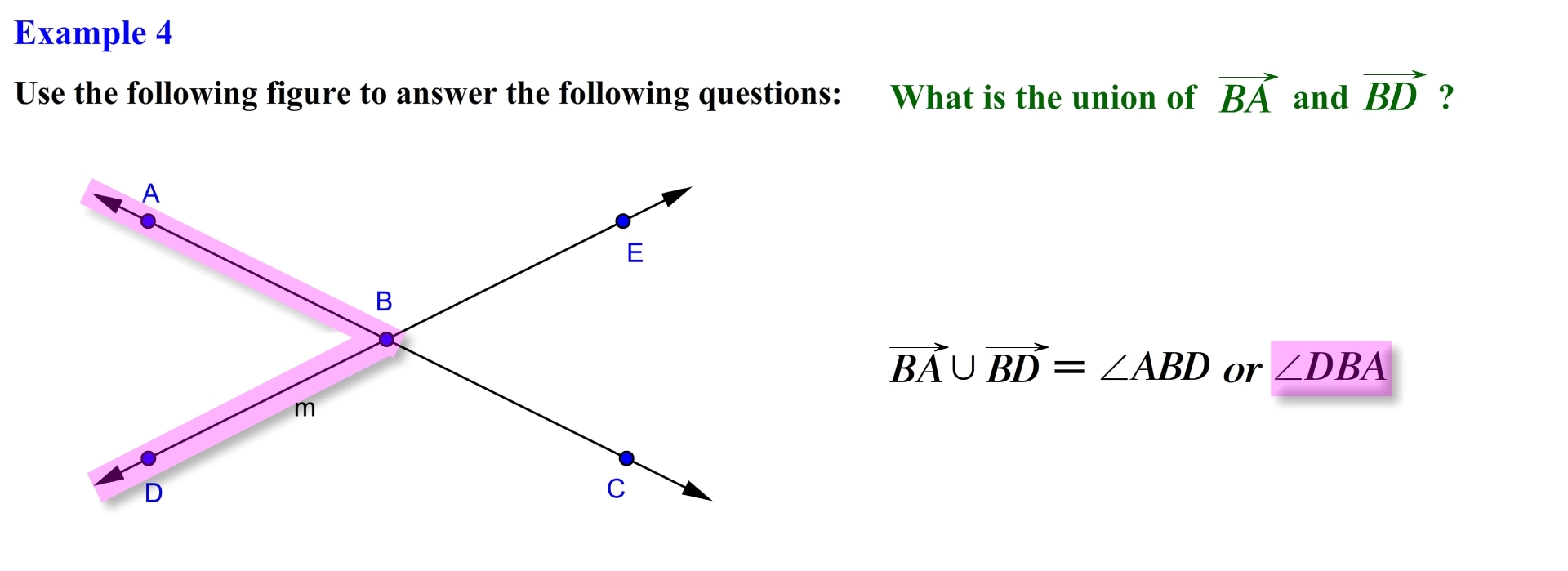
First let’s locate each of the rays, ray BA is located here and ray BD is located here, you can think of a union as merger between these two rays, we want to include all the points on ray BA or BD or in both. Recall that an angle is formed when two rays have a common point of intersection called the vertex this is essentially what happens when we form the union of these two rays, therefore the union of ray BA and ray BD is equal to angle ABD or DBA. Let’s move along to the next example.
Using set notation this problem translates to the following expression:
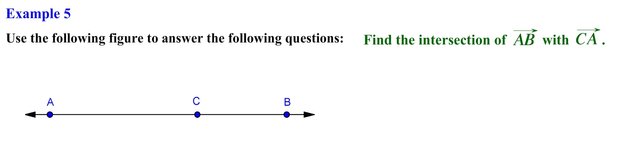
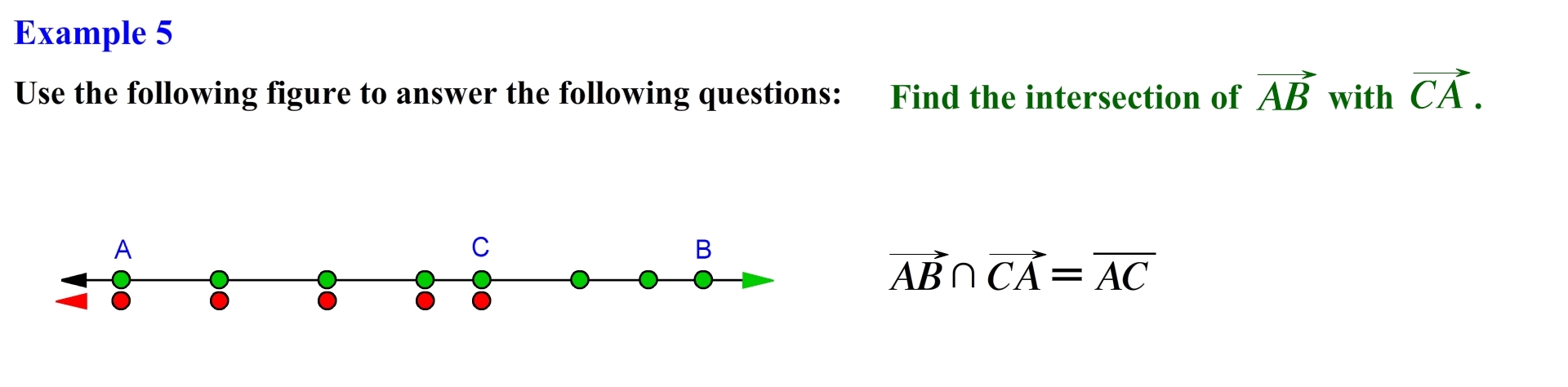
Once again lets identify the set of points located on ray AB, then we need to identify the set of points on ray CA, now it’s just matter of finding where the set of points of these two rays intersect, we see that the set of points on both rays start intersecting at point A and end at point C, in essence the set of points intersect along a common line segment in this case line segment AC. So the intersection of these two rays is equal to line segment AC. Alright let’s end the post with the final example.
Using set notation this problem translates to the following expression:
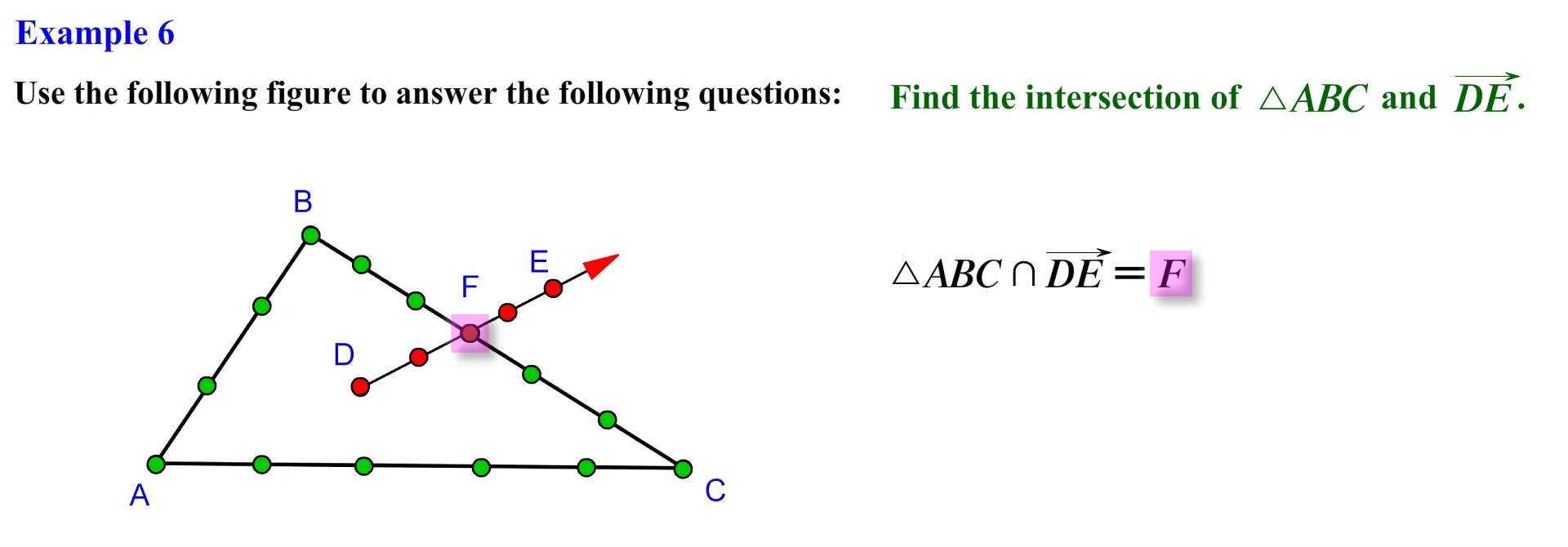
The set of all points located on triangle ABC are represented as follows, and the set of all points located on ray DE are represented as follows, for this problem we are looking for the intersection of these two set of points. Notice that both sets intersect at a common point in this case they intersect at point F, so the intersection of triangle ABC and ray DE is the set containing point F.
Alright in our next post we will continue covering slightly more challenging examples involving the union and intersection of geometric figures.


I like post
thanks to you for share 😊😊