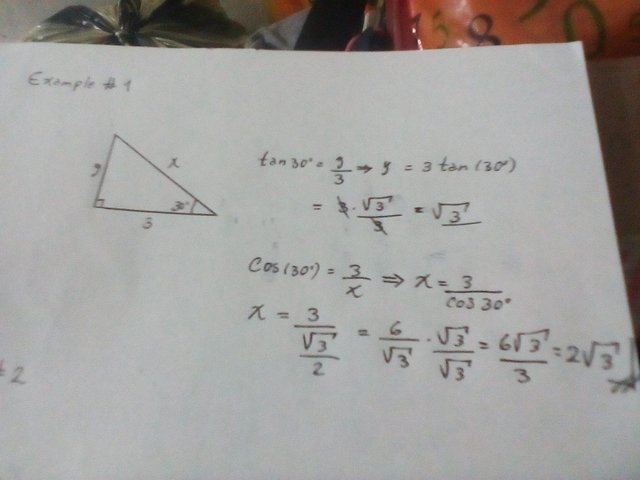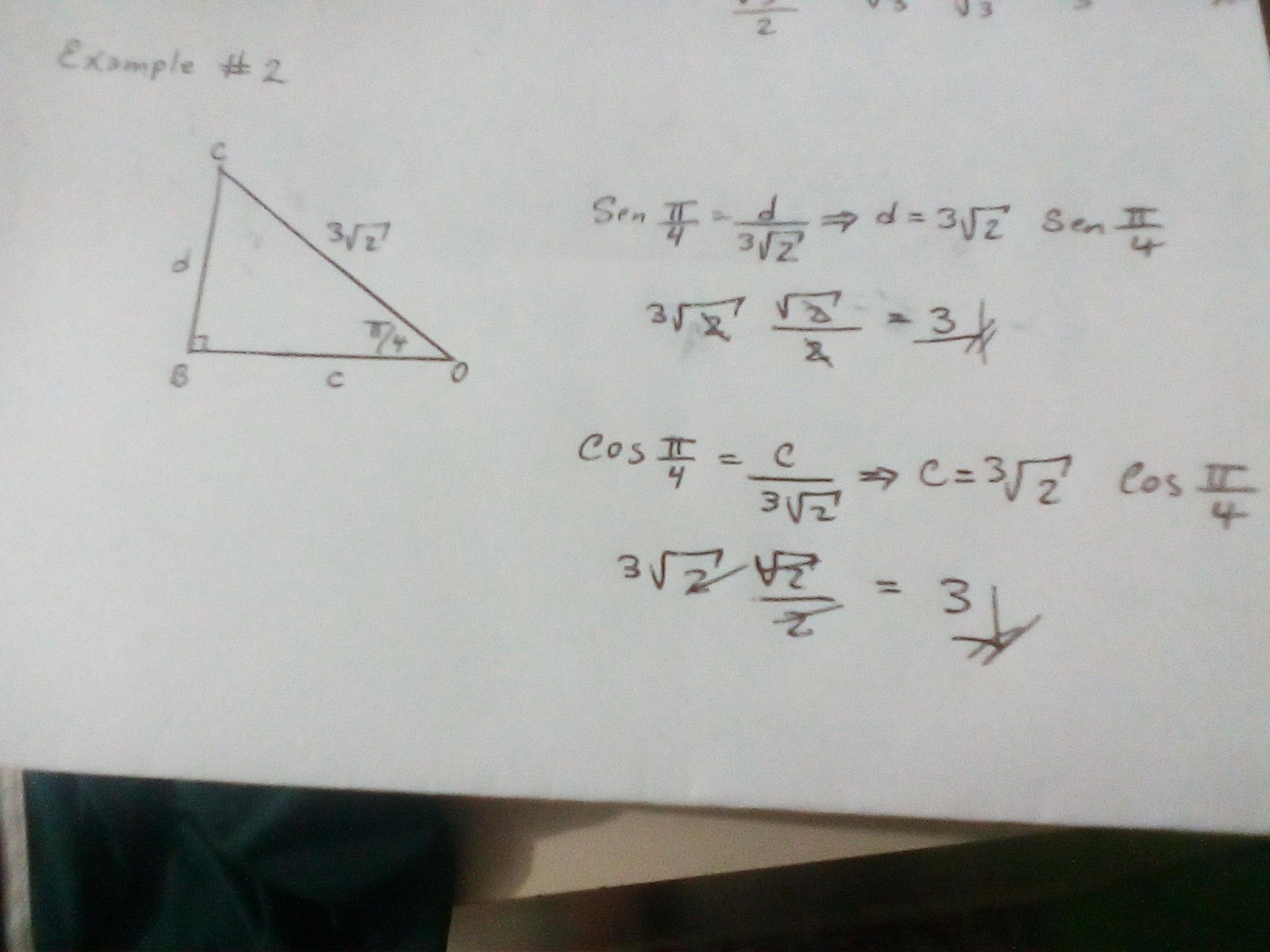Hello friends of steemit continuing with my mathematical explanations, today in this post I will talk about the trigonometric functions, all the components that comprise it, their respective graphics and I will also establish some demonstration exercises on how the trigonometric function is applied.

Trigonometric Function

In mathematics, trigonometric functions are the functions established in order to extend the definition of trigonometric ratios to all real and complex numbers.

The trigonometric functions are of great importance in physics, astronomy, cartography, nautical, telecommunications, the representation of periodic phenomena, and many other applications.

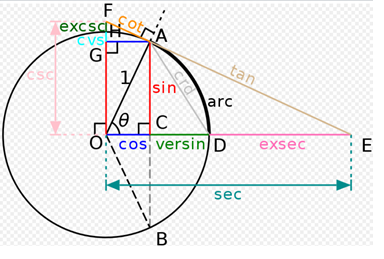
All trigonometric functions of an angle θ can be constructed geometrically in relation to a circumference of radius unit of center O.

Basic concepts

Trigonometric functions are commonly defined as the quotient between two sides of a right triangle, associated with its angles. Trigonometric functions are functions whose values are extensions of the concept of trigonometric ratio in a right triangle drawn on a unit circumference (of unit radius). More modern definitions describe them as infinite series or as the solution of certain differential equations, allowing their extension to positive and negative values, and even complex numbers.

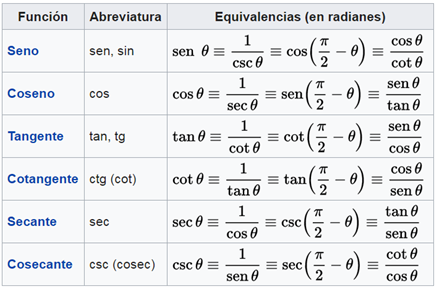
There are six basic trigonometric functions. The last four are defined in relation to the first two functions, although they can be defined geometrically or through their relationships. Some functions were common in the past, and appear in the first tables, but are not currently used; for example the verseno (1 - cos θ) and the exsecante (sec θ - 1).

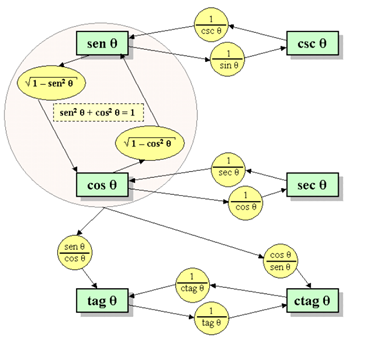
Fundamental trigonometric identities.

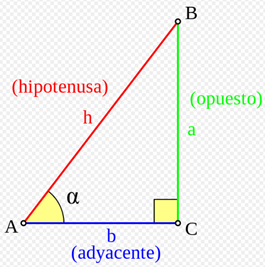
Definitions regarding a right triangle

To define the trigonometric ratios of the angle: {\ displaystyle \ alpha} \ alpha, from vertex A, we start with an arbitrary right triangle that contains this angle. The name of the sides of this right triangle that will be used in the following will be:

The hypotenuse (h) is the side opposite the right angle, or side of greater length of the right triangle.
The opposite leg (a) is the side opposite the angle {\ displaystyle \ alpha} \ alpha.
The adjacent leg (b) is the side adjacent to the angle {\ displaystyle \ alpha} \ alpha.
All the triangles considered are in the Euclidean Plane, so the sum of their internal angles is equal to π radians (or 180 °). Consequently, in any right triangle the non-right angles are between 0 and π / 2 radians. The definitions given below strictly define the trigonometric functions for angles within that range:

1. The sine of an angle is the relation between the length of the opposite leg and the length of the hypotenuse:

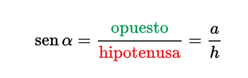
The value of this relation does not depend on the size of the right triangle that we choose, as long as it has the same angle alpha, in which case it is similar triangles.

1. The cosine of an angle is the relation between the length of the adjacent leg and the length of the hypotenuse:

1. The tangent of an angle is the relation between the length of the opposite leg and that of the adjacent one:

1. The cotangent of an angle is the relation between the length of the adjacent leg and that of the opposite leg:

1. The secant of an angle is the relation between the length of the hypotenuse and the length of the adjacent leg:

1. The cosecant of an angle is the relation between the length of the hypotenuse and the length of the opposite leg:

Trigonometric functions of remarkable angles

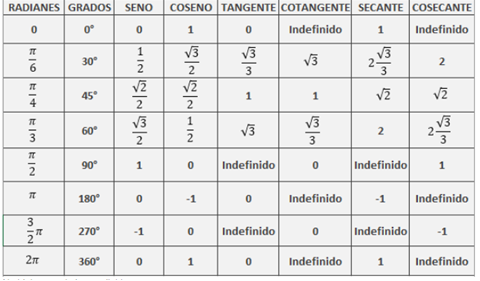
Definition for any real number

It is not possible to use the definition given above, a cosine of alpha for values of alpha less than or equal to 0 or values greater than or equal to π / 2, as it could not be construct a right triangle such that one of its angles measure alpha radians. To define the values of these functions for values between 0 and 2π, then a unit circumference will be used, centered on the coordinate origin of the Cartesian plane. The trigonometric functions cosine and sine will be defined as the abscissa (x) and the ordinate (y), respectively, of a point P of coordinates (x, y), belonging to the circumference, being alpha angle, measured in radians, between the positive semiaxis x and the segment joining the origin with P.

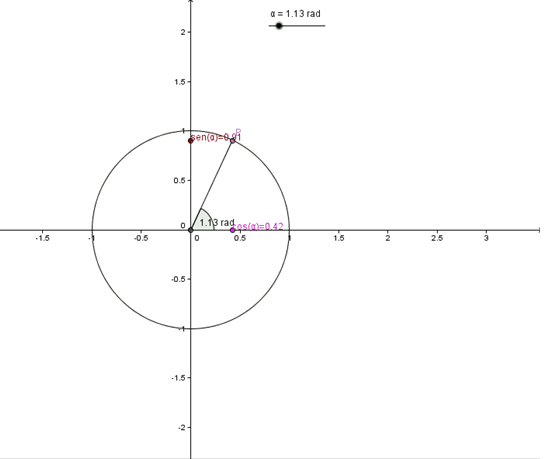
It can be observed that these functions take values between -1 and 1. Note that for values between 0 and π / 2, the values obtained for the sine and the cosine with this definition coincide with those obtained using the notion of trigonometric ratio. If the value of x is outside the interval [0,2π], it can be decomposed as x = 2kπ + x 'where k is an integer and x' a value between 0 and 2π. The same values of sine and cosine will be assigned to x as those assigned to x ', since x can be interpreted as a coterminal angle with x', and therefore, the coordinates of point P will be the same in both cases.

Graphic representation

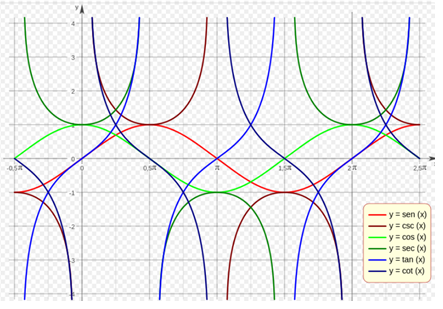
Graphic representation in a Cartesian coordinate system.

Trigonometric functions of double angle

Knowing the trigonometric functions of the sum of two angles, we can determine the trigonometric functions of double angle by stating that alpha = beta

For the formula of the cosine of the double angle two other alternative forms can be presented with the use of Pythagorean identities: Converting (alpha to terms of sin (alpha), or converting sen (alpha) to terms of cos (alpha):

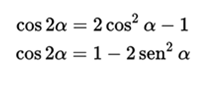
For the tangent of the double angle, proceed in the same way:

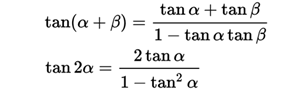
For products with two complementary sinusoidal functions, you have to:

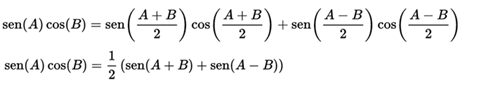
And for the alternative case:

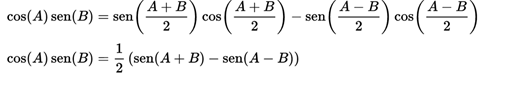
Analytical definitions

The most frequent analytical definition within the real analysis is made from differential equations. Using the geometry and the properties of the limits, it can be shown that the derivative of the sine is the cosine and the derivative of the cosine is the sine with a negative sign. (Here, as is generally done in calculation, all angles are measured in radians).

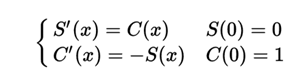
Picard-Lindelöf's theorem of existence and uniqueness of the differential equations leads to the existence of the previous functions that are respectively called sine and cosine, that is:

This analytical definition of trigonometric functions allows a non-geometric definition of the number π, namely, that number is the minimum positive real number that is a zero of the sine function.

Power series

From the previous definition it can be established that the sine and cosine functions are analytic functions whose Maclaurin series is given by:

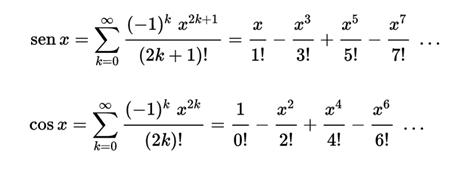
These identities are sometimes used as the definitions of the sine and cosine functions. They are often used as the starting point for the rigorous treatment of trigonometric functions and their applications (for example in the Fourier Series), because the theory of infinite series can be developed from the base of the system of real numbers, independently of any geometric consideration. The differentiability and continuity of these functions is then established from the definitions of series by itself.

Relationship with the complex exponential

There is an important relationship between the exponentiation of complex numbers and the trigonometric functions according to Euler's formula:

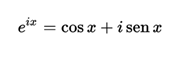
This relationship can be proved using the Taylor series development for the exponential function and the one obtained in the previous section for the sine and cosine functions. Separating now real and imaginary in the previous expression are the definitions of sine and cosine in terms of complex exponentials:

From differential equations

The sine and cosine functions satisfy equality:

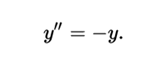
That is, the second derivative of each function is the function itself with inverse sign. Within the functional space of two dimensions V, which consists of all the solutions of this equation, the dependent variables, together, can form the basis of V. This method to define the sine and cosine functions is essentially equivalent to using Euler's formula . In addition, this differential equation can be used not only to define the sine and the cosine, with it you can also test the trigonometric identities of the sine and cosine functions.

In addition, the observation that the sine and the cosine satisfy y '' = -y implies that they are functions proper to the operator of the second derivative.

The tangent function is the only solution of the nonlinear differential equation

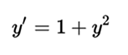
satisfying the initial condition and (0) = 0. There is an interesting visual proof that the tangent function satisfies this differential equation.

Inverse trigonometric functions

The three inverse trigonometric functions commonly used are:

Arcosine is the inverse function of the sine of an angle. The geometric meaning is: the arc whose sine is said value.
The real arcosine function is a function {1,-1} , {0,2Pi} that is, it is not defined for any real number. This function can be expressed by the following Taylor series:

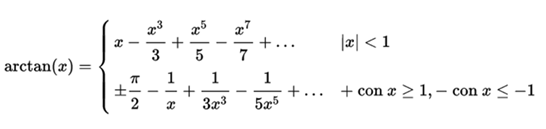
• Arcocosine is the inverse function of the cosine of an angle. The geometric meaning is: the arc whose cosine is said value.
  It is a function similar to the previous one, in fact it can be defined as:

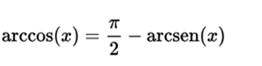
• Arctangent is the inverse function of the tangent of an angle. The geometric meaning is: the arc whose tangent is said value.
  Unlike the previous ones, the arctangent function is defined for all reals. Its expression in the form of series is:

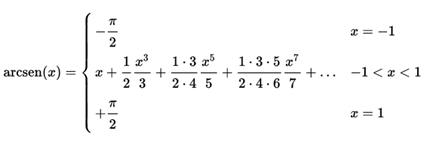
Graphic representation

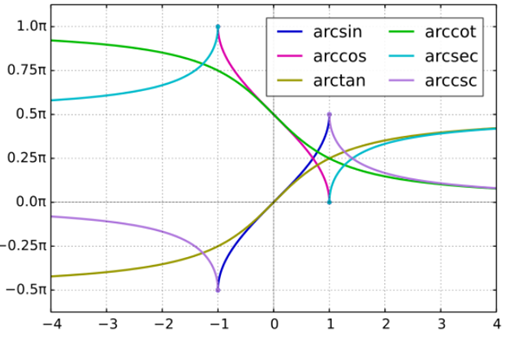
Generalizations

The hyperbolic functions are the analog of the trigonometric functions for an equilateral hyperbola. In addition, the sine and cosine of a pure imaginary number can be expressed in terms of hyperbolic functions.
The elliptic functions are a bi-periodic generalization of the trigonometric functions that in the complex plane are only periodic on the real axis. In particular, trigonometric functions are the limit of the Jacobi elliptic functions when the parameter they depend on tends to zero.

Example of basic trigonometric exercises where the trigonometric properties are applied to obtain the following results:

Source:

https://es.wikipedia.org/wiki/Funci%C3%B3n_trigonom%C3%A9trica

Bibliography :

Spiegel, M. & Abellanas, L .: "Formulas and tables of applied mathematics", Ed. McGraw-Hill, 1988.