Hello friends of steemit continuing with my publications on the science of mathematics today I want to refer to the fundamental concept of calculation and mathematical analysis I speak of integration, in this post I will establish basic concepts, properties of integration, theorems and also apply in some example the properties to solve some integral exercises.

The integration

Integration is a fundamental concept of calculation and mathematical analysis. Basically, an integral is a generalization of the sum of infinite addends, infinitely small.

The integral calculus, framed in the infinitesimal calculus, is a branch of mathematics in the process of integration or antiderivation. It is very common in engineering and science; It is mainly used for the calculation of areas and volumes of regions and solids of revolution.

It was used for the first time by scientists such as Archimedes, René Descartes, Isaac Newton, Gottfried Leibniz and Isaac Barrow. The works of the latter and the contributions of Newton generated the fundamental theorem of integral calculus, which proposes that derivation and integration are inverse processes.

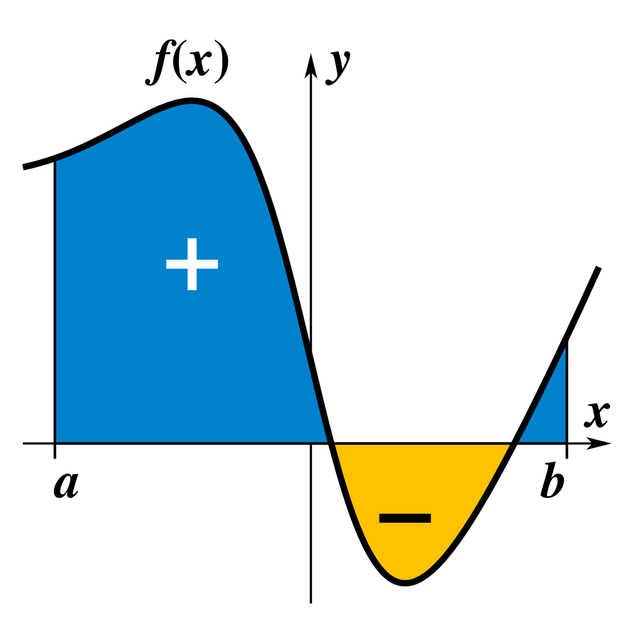
The definite integral of a function represents the area limited by the graph of the function, in a Cartesian coordinate system with a positive sign when the function takes positive values and a negative sign when it takes negative values.

Theory

Given a function f (x) of a real variable x and a range [a, b] of the real line, the integral is equal to the area of the region of the xy plane and limited between the graph of f, the x axis, and the lines verticals x = ayx = b, where the areas below the x axis are negative.

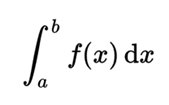
The word "integral" can also refer to the notion of primitive: a function F, whose derivative is the given function f. In this case it is called indefinite integral, while the integrals treated in this article are the defined integrals. Some authors maintain a distinction between primitive and indefinite integrals.

The principles of integration were formulated by Newton and Leibniz at the end of the 17th century. Through the fundamental theorem of calculus, which the two developed independently, the integration is connected to the derivation, and the definite integral of a function can be easily calculated once an antiderivative is known. Integrals and derivatives became basic calculation tools, with numerous applications in science and engineering.

Bernhard Riemann gave a rigorous definition of the integral. It is based on a limit that approximates the area of ​​a curvilinear region by splitting it into small vertical pieces. At the beginning of the 19th century, more sophisticated notions of the integral began to appear, where the types of functions and the domains on which integration is made are generalized. The curvilinear integral is defined for vector functions of a variable, and the integration interval [a, b] is replaced by the parameterization of the curve on which it is being integrated, which connects two points of the plane or space . In a surface integral, the curve is replaced by a piece of a surface in three-dimensional space.

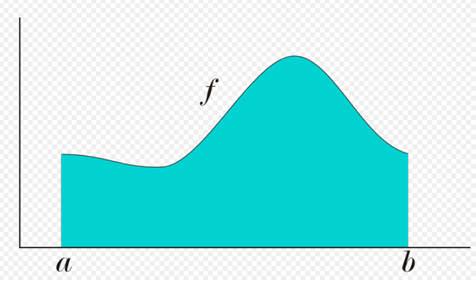
f(x) dx is interpreted as the area under the curve of f, between a and b

Properties of the integration

Linearity

• The set of Riemann functions integrable in a closed interval [a, b] form a vector space with the addition operations (the sum function of two others is the function that corresponds to the sum of the images of this point at each point for each of the other two) and multiplication by a scalar. The integration operation.

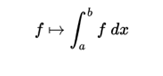
It is a linear functional of this vector space. Thus, first of all, the set of integrable functions is closed with the linear combination, and secondly, the integral of a linear combination is the linear combination of the integrals,

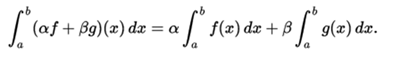
• Similarly, the set of real Lebesgue functions integrable in a given metric space E, with the measure μ is closed with respect to the linear combinations and therefore form a vector space, and the integral of Lebesgue

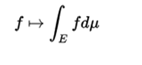
is a linear functional of this vector space, so that

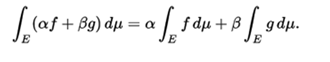
• More generally, if we take the vector space of all the measurable functions on a metric space (E, μ), which take values in a fully compact local topological vector space V over a locally compact topological field K, f: E → V. Then you can define an abstract integration application that assigns to each function f an element of V or the symbol ∞

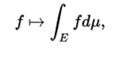
which is compatible with linear combinations. In this situation, linearity is held for the subspace of the functions, whose integral is an element of V (that is, the "finite" integrals). The most important cases arise when K is R, C, or a finite extension of the field Qp of p-adic numbers, and V is a vector space of finite dimension on K, and when K = C and V is a complex Hilbert space .
Linearity, along with some natural properties of continuity and normalization for certain classes of "simple" functions, can be used to give an alternative definition of integral. This is Daniell's approach to the case of real functions in an X set, generalized by Bourbaki to functions that take values in a topologically compact vector space.

Inequalities with integrals

Several general inequalities are verified for integrable Riemann functions defined in a closed and bounded interval [a, b] and can be generalized to other notions of integral (Lebesgue and Daniell).

• Upper and lower bounds. A function f integrable in [a, b], is necessarily bounded in the interval. Therefore there are two real numbers m and M such that m ≤ f (x) ≤ M for all x of [a, b]. Given that the upper and lower summations of f over [a, b] are also bounded for m (b - a) and M (b - a) respectively, it follows that

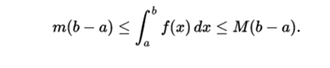
• Inequalities between functions. If f (x) ≤ g (x) for all x of [a, b] then each of the upper and lower summations of f are bounded inferiorly and superiorly by the upper and lower summations of g respectively. A) Yes

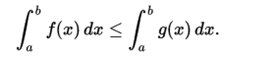
This is a generalization of the above inequalities, since M '(b - a) is the integral of the constant function with value M in the interval [a, b].

• Subintervals If [c, d] is a subinterval of [a, b] and f (x) is not negative for all x, then

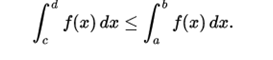
• Products and absolute values of functions. If f and g are two functions, then we can use their product, powers and absolute values:

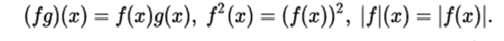
If f is Riemann integrable in [a, b] then the same is true for | f |, and

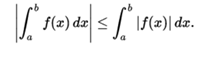
Moreover, if f and g are both integrable Riemann then f , g , and fg are also Riemann integrable, and

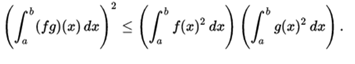
This inequality is known as the Cauchy-Schwarz inequality, and plays a fundamental role in the theory of Hilbert spaces, where the right-hand side is interpreted as the scalar product of two integrable functions f and g in the interval [a, b] .
Hölder's inequality. If p and q are two real numbers, 1 ≤ p, q ≤ ∞ with 1 / p + 1 / q = 1, and f and g are two integrable Riemann functions. Then the functions | f | p and | g | q are also integrable and the Hölder inequality is fulfilled:

For the case of p = q = 2, the Hölder inequality becomes the Cauchy-Schwarz inequality.
Inequality of Minkowski. If p ≥ 1 is a real number and f and g are integrable Riemann functions. Then | f | p, | g | p and | f + g | p are also Riemann integrables and the inequality of Minkowski is fulfilled:

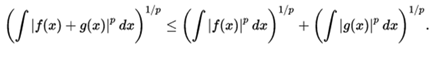
An inequality analogous to this for the Lebesgue integral is used in the construction of the spaces.

Fundamental theorem of calculation

The fundamental theorem of calculus is the assertion that derivation and integration are inverse operations: if a continuous function is first integrated and then derived, the original function is recovered. An important consequence, sometimes called the second fundamental theorem of calculation, allows to calculate integrals based on using a primitive of the function to be integrated.

Statement of theorems

Fundamental theorem of the calculation. Let f be an integrable real function defined in a closed interval [a, b]. If F is defined for each x of [a, b] by

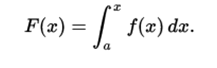
then F is continuous in [a, b]. If f is continuous in x of [a, b], then F is derivable in x, and F '(x) = f (x).
Second fundamental theorem of the calculation. Let f be a real, integrable function defined in a closed interval [a, b]. If F is a function such that F '(x) = f (x) for all x of [a, b] (that is, F is a primitive of f), then

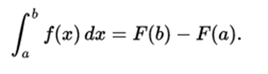
Corollary. If f is a continuous function in [a, b], then f is integrable in [a, b], and F, defined by

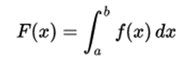
is a primitive of f in [a, b]. Further,

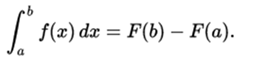
Surface integrals

A surface integral is a definite integral calculated on a surface (which can be a set curved in space, it can be understood as the double integral analogous to the line integral.) The function to be integrated can be a scalar field or a vector field The value of the surface integral is the weighted sum of the field values ​​at all points on the surface.This can be achieved by dividing the surface into surface elements, which provide the partition for the Riemann summations. .

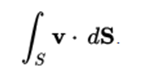
As an example of the applications of the surface integrals, we can consider a vector field v on a surface S; that is, for each point x of S, v (x) is a vector. Imagine that you have a fluid flowing through S, so that v (x) determines the velocity of the fluid at point x. The flow rate is defined as the amount of fluid flowing through S in the unit of time. To find the flow, we must calculate the scalar product of v by the normal unit vector to the surface S at each point, which will give us a scalar field, which we integrate on the surface:

The definition of surface integrals rests on the division of the surface into small surface elements.

Below are some examples of integral exercises, applying the basic properties of integration:

References

1 . In the case of the functions to which the Riemann definition applies, the results coincide.
2 . Burton, David M. (2005). The History of Mathematics: An Introduction (6th ed.), McGraw-Hill, p. 359
3 . Leibniz, Gottfried Wilhelm (1899) (Gerhardt, Karl Immanuel, ed.). Der Briefwechsel von Gottfried Wilhelm Leibniz mit Mathematikern. Erster Band, Berlin: Mayer & Müller, p. 154
4 . Cajori, Florian (1929). A History of Mathematical Notations, Vol. II, Open Court Publishing, pp. 247-252
5 . Fourier, Jean Baptiste Joseph (1822). Théorie analytique de la chaleur, Chez Firmin Didot, père et fils, p. §231,
W3C (2006). Arabic mathematical notation

Bibliography

• Apostol, Tom M. (1967). Calculus, Vol. 1: One-Variable Calculus with an Introduction to Linear Algebra (2nd edition). John Wiley & Sons.
• Bourbaki, Nicolas (2004). Integration I. Springer. ISBN 3-540-41129-1 .. In particular chapters III and IV.
• Burton, David M. (2005). The History of Mathematics: An Introduction (6th edition). McGraw-Hill. p. 359.
• Cajori, Florian (1929). A History Of Mathematical Notations Volume II. Open Court Publishing. pp. 247-252.
• Dahlquist, Germund; Björck, Åke (forthcoming). «Chapter 5: Numerical Integration». Numerical Methods in Scientific -
  Computing. Philadelphia: SIAM. Archived from the original on June 15, 2007.
• Folland, Gerald B. (1984). Real Analysis: Modern Techniques and Their Applications (1st edition). Wiley-Interscience.
• Fourier, Jean Baptiste Joseph (1822). Théorie analytique de la chaleur. Chez Firmin Didot, père et fils. p. §231.
• Available in English as Fierier, Joseph (1878). The analytical theory of heat. Freeman, Alexander (trans.). Cambridge University Press. pp. 200-201.
• Heath, T. L., ed. (2002). The Works of Archimedes. Dover ISBN 978-0-486-42084-4.
• (Originally published by Cambridge University Press, 1897, based on J.L. Heiberg's Greek version.)