Hi friend of steemit, referring to my explanations about the science of mathematics, today I will talk about a topic of great importance, and we will talk about multiplication and all the properties that this binary operation allows us to perform.

The multiplication and its properties

Multiplication is a binary operation that is established in a numerical set.1 As in the case of natural numbers, it consists of adding a number as many times as another number indicates. Thus, 4 × 3 (read "four multiplied by three" or simply "four times three") is equal to adding three times the value 4 by itself (4 + 4 + 4). It is an operation different from the addition, but equivalent; It is not equal to a repeated sum, they are only equivalent because they allow to achieve the same result. The multiplication is associated to the concept of geometric area.

Potentiation is a particular case of multiplication where the exponent indicates the times a number should multiply by itself.

The result of the multiplication of several numbers is called product. The numbers that are multiplied are called factors or coefficients, and individually: multiplying (number to add or number that is multiplying) and multiplier (times the multiplicand is added). Although this differentiation in some contexts can be superfluous when in the set where the product is defined we have the commutative property of multiplication (for example, in the numerical sets), but it can be useful when it is used to refer to the multiplier of an expression algebraic (example: in 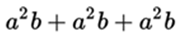o 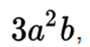is the multiplier or coefficient, while the monomial 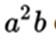is the multiplying).

In modern algebra the denomination "quotient" or "multiplication" with its usual notation "·" is usually used to designate the external operation in a module, to also designate the second operation that is defined in a ring (the one for which it is not defined the inverse element of 0), or to designate the operation that endows a set of group structure. The inverse operation of multiplication is division.

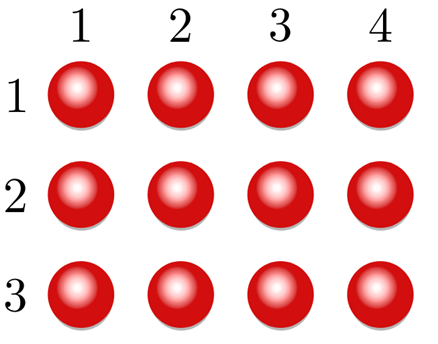
Commutative property:

3 × 4 = 12 = 4 × 3

twelve elements can be arranged in three rows of four, or four columns of three.

Notation

The multiplication is indicated by a cross (×) or the midpoint (·). In the absence of these characters the asterisk (*) is usually used, especially in computing (this use has its origin in FORTRAN), but it is discouraged in other areas and should only be used when there is no other alternative. Sometimes the letter x is used (x), but this is inadvisable because it creates unnecessary confusion with the letter that is normally assigned to an unknown in an equation. Finally, the multiplication sign can be omitted unless numbers are multiplied or confusion can be generated about the names of the unknowns, constants or functions (for example, when the name of some unknown has more than one letter and could be confused with the product of two others). Grouping signs such as parentheses (), brackets [] or curly braces {} are also commonly used. This is mostly used to multiply negative numbers with each other or by positive numbers.

If the factors are not written individually but belong to a list of elements with some regularity, the product can be written by an ellipsis, that is, by explicitly writing the first and last terms (or in case of a product of infinite terms). only the first ones), and substitute the others for some ellipses. This is analogous to what is done with other operations applied to infinite numbers (such as sums).

Thus, the product of all natural numbers from 1 to 100 can be written:

1.2.....99.100

while the product of even numbers between 1 and 100 would be written:

2 . 4 . 6 . . . . 100

This can also be denoted by writing the ellipsis in the middle part of the text line:

1 . 2. . . . . . 99 . 100

In any case, it must be clear what the omitted terms are.

Finally, the product can be denoted by the producer symbol, which comes from the Greek letter Π (uppercase Pi).

This is defined as:

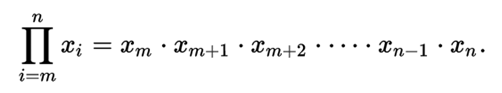
The subscript ( i) indicates a variable that traverses whole numbers from a minimum value (m, indicated in the subscript) and a maximum value (n, indicated in the superscript).

Definition

The multiplication of two integers n and m is expressed as:

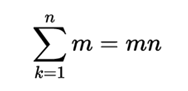
This is just a way of symbolizing the expression "add myself n times". It can facilitate understanding by expanding the previous expression:

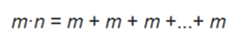
such that there are n addends. For example:

• 5 × 2 = 5 + 5 = 10
• 2 × 5 = 2 + 2 + 2 + 2 + 2 = 10
• 4 × 3 = 4 + 4 + 4 = 12
• m · 6 = m + m + m + m + m + m = 6m
• m · 5 = m + m + m + m + m = 5m

The product of infinite terms is defined as the product limit of the first n terms when n grows indefinitely.

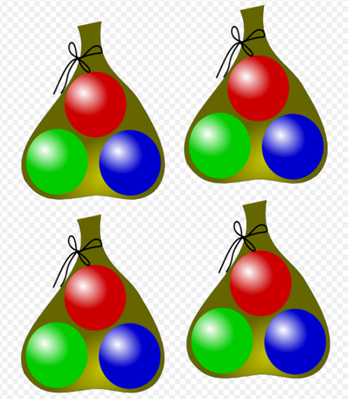
Four bags of three balloons gives a total of twelve balloons (3 × 4 = 12).

Recursive definition

In the case of multiplication of natural numbers ℕ = {0,1,2,3. ..., n, ...} the recursive definition of multiplication can be applied, which comprises these two steps:

m · 0 = 0

m · (n + 1) = m.n + m.

Where m and n are natural numbers, the principle of induction is applied to the number n, which initially is n = 0, then assuming that it is true for n, it is inferred that it is also fulfilled for n + 1.

The following basic propositions are deduced:

Existence of the identity element,n . 1 = n all natural number n.
Associative property, ( m .n ) . p = m . ( n . p) for any m, n, p natural numbers.
Commutative property: m .n = m .n , for n and n any natural number.
Distributive property with respect to the addition:

m ( I +n ) = m . I + m .n = (I+n ) . m

There are no divisors of zero: m . n = 0 implies that at least one of the factors is equal to zero

To indicate the product of two natural numbers a point is used between the two factors, a cross between them, the simple juxtaposition of the literal factors or, one factor and the other in parentheses or the two factors in parentheses

Product of whole numbers

It is an integer m that is calculated as follows:

If n> 0 and p> 0 then m = n. p, positive factors
If n <0 and p <0 then m = InI IPI, negative factors
If n> 0 and p <0 or n <0 and p> 0 then m = -InI IpI, one positive factor and the other negative.

If n = 0 and p = 0 then m = 0 = n. p. At least one zero factor.

The product of the integers is based on the product of the natural numbers and the absolute value is taken into account.

Fractions product

The fraction ![mul8.png]
() is the product of the fractions 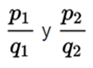who meet the equality

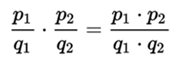
It is assumed that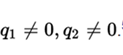

Radical product

In the case of second-degree or quadratic radicals:

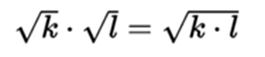
In the same way there is product of reals, expressed in decimals; of real numbers of the form a + / b being a rational number and b a positive rational not perfect square. Then product of complex numbers, Gaussian numbers.

Multiplication of numbers from 0 to 10. Each line drawn represents a multiplicand. Axis x = multipliators. Axis y = products.

Properties

For natural numbers, integers, fractions and real and complex numbers, multiplication has certain properties:

Lock property

The multiplication of two or more natural numbers results in another natural number example: 33 * 2 = 66

Commutative property

The order of the factors does not alter the product.

x. y = y . x

Associative property

Only expressions of multiplication or addition are invariant with respect to the order of operations.

(x . y ). z = x . (y . x )

Distributive property

The total of the sum of two numbers multiplied by a third number is equal to the sum of the products between the third number and each summand.

x . (y + z )= (z . y ) + (x . z )

Identity element (neutral)

The multiplicative identity is 1; the product of every number multiplied by 1 is itself. This is known as identity property.

x . 1 = x

Element zero (absorbent)

Any number multiplied by zero gives as a product zero. This is known as the zero property of multiplication.

x . 0 = 0

0 . x = 0

Denial

Less one multiplied by any number is equal to the opposite of that number.

(-1 ) . x = (- x )

Less one multiplied by minus one is one.

( - 1 ) . ( - 1 )= 1

The product of natural numbers does not include negative numbers.

Reverse element

Every number x, except zero, has a multiplicative inverse, 1 / x , such that

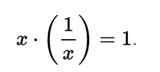
Product of negative numbers

The product of negative numbers also requires a little reflection. First, consider the number -1. For any positive integer m:

( - 1 )m =( - 1) + ( - 1 ) + .... +( - 1 ) = - m

This is an interesting result that shows that any negative number is no more than a positive number multiplied by -1. So the multiplication of any integers can be represented by the multiplication of positive integers and factors -1. The only thing that remains to be defined is the product of ( - 1 ) ( - 1 ) :

( - 1 ) ( - 1) = - (- 1 ) = 1

In this way, the multiplication of two integers is defined. Definitions can be extended to ever larger sets of numbers: first the set of fractions or rational numbers, then all real numbers and finally complex numbers and other extensions of real numbers.

Connection with geometry

From a purely geometric point of view, the multiplication between 2 values produces an area that is representable. In the same way, the product of 3 values produces an equally representative volume.

Extensions

In mathematics, product is synonymous with multiplication.

Some binary operations carried out in specialized contexts are also called product.

• Scalar product is a binary operation between elements of a vector space that results in an element of the underlying field. The most relevant case is that of point product.

• Vector product or cross product is an operation between vectors of a 3-dimensional Euclidean space that results in another vector.

• Mixed product or triple scalar product is a product that combines the vector product and the scalar product.
  Matrix product is a binary operation between matrices.

• Cartesian product is an operation between sets whose result are ordered pairs of respective elements.

• Topology product is a topology constructed in a Cartesian product of topological spaces.

• Topology box is another topology constructed in a Cartesian product of topological spaces that coincides with the previous one in finite products.

• Foreign product is a generalization of the vector product.

• Direct product is an abstraction that allows to define algebraic structures in products of other algebraic ones (usually Cartesian products)

• Producer Notation to denote an arbitrary product of terms.

• Product (category theory) is an abstract generalization of the products found in different algebraic structures.
  The term product is also related to

• Rule of the product, a method to calculate the derivative of a product of functions.

• Principle of the product, one of the fundamental principles of counting.

• Empty product is the product of zero factors.

Some example of exercises applying the properties of multiplication:

Source : https://es.wikipedia.org/wiki/Multiplicaci%C3%B3n

References

1 . Cotlar- Ratto of sadosky. «Introduction to algebra / Notions of linear algebra»
2 . Schaumm editions. «Modern algebra»
3 . A. Adrian Albert. "Advanced algebra"
4 . Tsipkin. «Mathematics Handbook»
5 . César Trejo «The concept of number». OAS edition.
6 . García Ardura «Exercises and problems of algebra»